Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Um curso de Cálculo Volume 2 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 8.2 - Ex. 12

12. Suponha que T x , y = 4 x 2 + 9 y 2 represente uma distribuição de temperatura no plano x y : T x , y   é a temperatura, que podemos supor em °C, no ponto x , y .

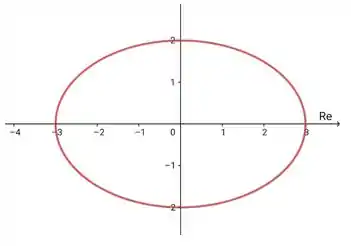
a) Desenhe a isoterma correspondente à temperatura de 36°C.

b) Deternine o ponto de mais baixa temperatura da reta   x + y = 1 .

Passo 1

Temperatura é   T x , y o enunciado pede para 36°C, então, é só substituir

  T x , y = 4 x 2 + 9 y 2

36 = 4 x 2 + 9 y 2

Dividindo por 36 em ambos os lados da equação,

1 = x 2 9 + y 2 4

Organizando para a forma reduzida da elipse,

1 = x 2 3 2 + y 2 2 2

Temos, uma elipse com eixo maior no x em 3 e eixo menor no y em 2, assim

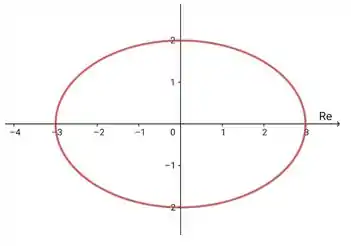
Passo 2

O ponto de mais baixa temperatura da reta   x + y = 1

  y = - x + 1

substituindo em T x , y = 4 x 2 + 9 y 2

T x , - x + 1 = 4 x 2 + 9 - x + 1 2

= 4 x 2 + 9 x 2 - 2 x + 1

= 4 x 2 + 9 x 2 - 18 x + 9

= 13 x 2 - 18 x + 9

Ponto de mínimo de uma função, deriva e iguala a zero

13 x 2 - 18 x + 9 ' = 0

2 ⋅ 13 x - 18 = 0

  x = 18 2 ⋅ 13 = 9 13

substituindo no y,

  y = - x + 1

  y = - 9 13 + 1

  y = 4 13

Então, o ponto de mais baixa temperatura é 9 13 , 4 13 .

Resposta

9 13 , 4 13

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Esboce o gráfico da função. f x , y = 10 - 4 x - 5 y
Encontre e esboce o domínio da função. f x , y = ln ⁡ ( 9 - x 2 - 9 y 2 )
Encontre e esboce o domínio da função. f x , y , z = ln ⁡ ( 16 - 4 x 2 - 4 y 2 - z 2 )
Esboce o gráfico da função. f x , y = y
Esboce o gráfico da função.25- f x , y = 1 - x 2