Enunciado
Cálculo - Um curso de Cálculo Volume 2 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 8.2 - Ex. 10
10. Sejam Desenhe a imagem de sendo
a) e b) e
c) e d) e
Passo 1
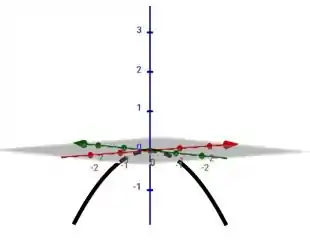
Substituindo os valores na letra a:
Imagem de :
Passo 2
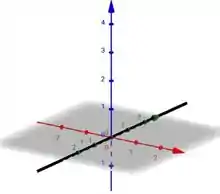
Substituindo os valores na letra b:
Imagem de
Passo 3
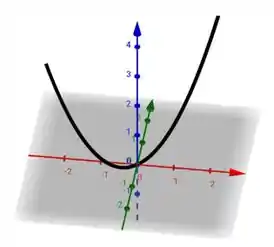
Substituindo os valores na letra c:
Imagem de
Passo 4
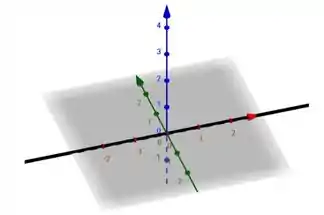
Substituindo os valores na letra d:
Imagem de
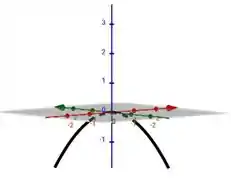
Resposta
Letra a
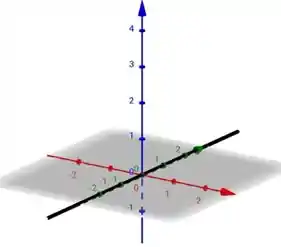
Letra b
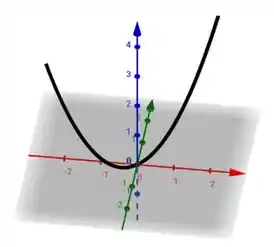
Letra c
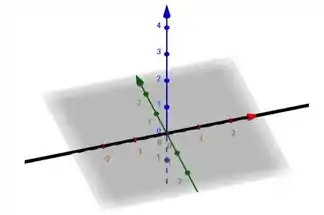
Letra d
Exercícios de Livros Relacionados
O índice de massa corporal é definido no exercício 39. Desenhe a curva de nível dessa função correspondente a alguém com 200 cm de altura e peso de 80 kg. Encontre os pesos e alturas de duas outras pe
Desenhe a curva de nível da função mostrando vários níveis. f x , y = l n ( x 2 + 4 y 2 )
Combine a função com seu gráfico (rotulado I-VI). Dê razões para suas escolhas. f x , y = 1 1 + x 2 + y 2 f x , y = 1 1 + x 2 y 2 f x , y = ln x 2 + y 2 f x , y = cos x 2 + y 2 f x , y = x y f x ,
Esboce o gráfico da função. f x , y = 2 - x 2 - y 2
Encontre e esboce o domínio da função. f x , y = x 2 + y 2 - 4