Enunciado
Cálculo - Diva Flemming - Cálculo A- Ed: 6º - Capítulo 4.16 - Ex. 84
Dada , mostra que é par e é ímpar. Usando uma ferramenta gráfica, esboçar o gráfico de e observando as simetrias.
Passo 1
Podemos identificar as funções pares como funções simétricas em relação ao eixo y – como se esse eixo fosse um espelho, e seus lados esquerdo e direito são iguais.
Pra essas funções também vale que .
Já as funções ímpares são o contrário: elas são antissimétricas em relação ao eixo y – ou seja, seus lados esquerdo e direito são simétricos, porém um de “cabeça pra baixo” em relação ao outro.
Pra essas funções, vai valer que .
Passo 2
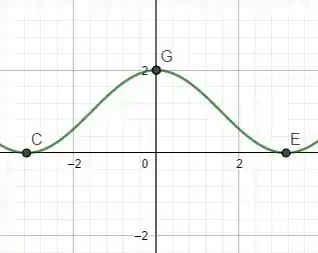
Pra , temos o seguinte esboço de gráfico. Repare como ele é totalmente simétrico em relação ao eixo das ordenadas (eixo y):
Passo 3
Já , que é a derivada de , vamos ter que vale:
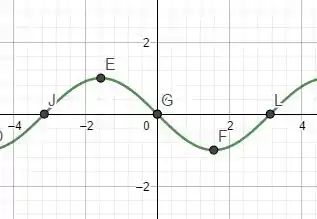
Para essa função, temos o seguinte esboço do gráfico. Repare que, em relação ao eixo y, passando pela origem, ele também é simétrico, só que um lado invertido em relação ao outro:
Resposta
Ei, a resposta está no passo a passo :)