Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Diva Flemming - Cálculo A- Ed: 6º - Capítulo 4.16 - Ex. 96

Dada a função y = f x = x 2 - 6 x + 5 definida para x ∈ [ 3 ,   + ∞ ) , desenvolver os seguintes itens:

  1. Determinar a função inversa y = g x = f - 1 ( x ) e identificar o domínio.
  2. Encontrar a equação da reta tangente à curva y = f ( x ) no ponto de abcissa 5 .
  3. Encontrar a equação da reta tangente à curva y = g ( x ) no ponto de abcissa 0 .
  4. Fazer uma representação gráfica dos resultados obtidos e identificar a relação estabelecida no Teorema 4.14 .

Passo 1

  1. Pra achar a inversa, a gente tem que “resolver” a função em x depois trocar por y . Assim ó:

    2. y = x 2 - 6 x + 5 ,     x ∈ [ 3 , +   ∞ )

    Vamos completar o quadrado...

    y = x 2 - 6 x + 9 - 9 + 5

    y = x - 3 2 - 4

    x - 3 2 = y + 4

    x - 3 =   y + 4

    x = 3 + y + 4    

    Agora a gente troca as letras...

    y = 3 + x + 4

    Essa é a função inversa, onde o domínio é D g = x ≥ - 4 .

    Passo 2

  2. Vamos derivar a função f para encontrarmos a equação da reta tangente:

    3. f ' x = 2 x - 6

    No ponto x = 5 ...

    f ' 5 = 4

    E nesse ponto, temos y = 0 .

    E agora montamos a equação da reta tangente:

    y - 0 = 4 x - 5

    y = 4 x - 20

    Passo 3

  3. Derivamos a função g x agora:

    4. g ' x = 1 2 x + 4

    Isso no ponto x = 0 ...

    g ' 0 = 1 4

    E o valor de y quando x = 0 é 5 .

    E aí a equação da reta tangente é:

    y - 5 = 1 4 ( x - 0 )

    y = 1 4 x + 5

    Passo 4

  4. Vamos ver isso graficamente agora:

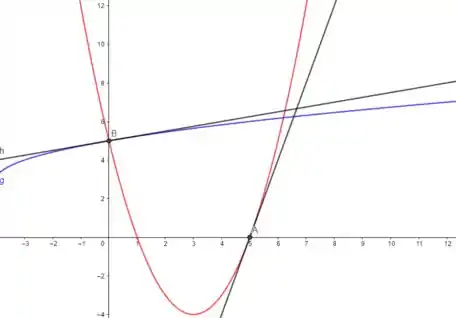
Vemos que as derivadas são inversas uma da outra, e a declividade também, como garante p teorema da Função Inversa citado.

Resposta

  1. y = 3 + x + 4 , x ≥ - 4
  2. y = 4 x - 20
  3. y = 1 4 x + 5
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Encontre f ' ( x ) pela Fórmula (7) e, então, por derivação logarítmica: f x = π x . t g ( x )
Encontre d y d x : y = l n ⁡ ( 1 - x e - x )
Encontre d y d x usando o método da derivação logarítimica: y = ( x 2 + 3 ) l n ( x )
Encontre d y d x : y = e x . t g ( x )
Encontre f ' ( x ) pela Fórmula (7) e, então, por derivação logarítmica: f x = π s e n ( x )