Enunciado

Cálculo - Diva Flemming - Cálculo A- Ed: 6º - Capítulo 4.16 - Ex. 86

Dada , calcular e verificar que e são periódicas de mesmo período. Usando uma ferramenta gráfica, esboçar os gráficos de e comprovando os resultados.

Passo 1

Para as funções trigonométricas periódicas como seno e cosseno, o número que acompanha diretamente o indica a periodicidade da função.

Assim, quando derivamos a nossa , verificamos que ela acaba tendo o mesmo número que acompanha o ().

Passo 2

Derivando, teremos:

Como dito, confirmamos: ambas as funções, a original e a derivada, tem como 2 o número que acompanha , que indica a periodicidade da função.

Passo 3

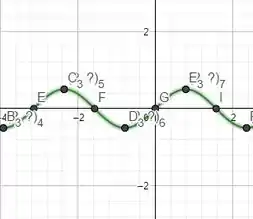
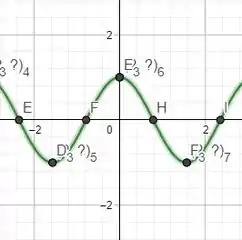
Os esboços dos gráficos dessas funções dão uma visualização melhor dos períodos. Lembre-se que os períodos nada mais são que a distância entre dois picos ou dois vales consecutivos.

Temos respectivamente os gráficos de e . Observe atentamente e perceba como os períodos são iguais!

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

(a) Mostre que, sobre um círculo de raio r o ângulo central θ que subentende um arco de comprimento 1,5 vezes o comprimento L de sua corda satisfaz a equação θ = 3s e nθ 2 (ver Figura Ex-33).(b) Use o

Use o Método de Newton para aproximar todos os valores reais de y que satisfazem a equação dada para o valor de x indicado. x y - cos ⁡ 1 2 x y = 0 ; x = 2

Uma anuidade é uma sequência de pagamentos iguais que são pagos ou recebidos em intervalos regulares de tempo. Por exemplo, podemos querer depositar quantias iguais ao final de cada ano em uma poupanç

34-Um satélite de observação pode ver somente uma parte da superfície da Terra. Ele tem sensores de horizonte que permitem calcular o ângulo θ , o qual pode ser visto na figura abaixo. Suponha que a T

29- Encontre todos os pontos no intervalo [ - 2 π ,2 π ] nos quais o gráfico de f tem uma reta tangente horizontal.a) f ( x ) = s e nx b) f ( x ) = x + cos ⁡ x c) f x = t g x d) f x = sec ⁡ x