Enunciado
Cálculo - Diomara - Cálculo Diferencial e Integral de Funções de Várias Variáveis- Ed: 3º - Capítulo 7.10 - Ex. 8
Seja a circunferência de raio , no plano , centrada no ponto . Se , determine o valor de para que:
Passo 1
Faaalaa jovem.. Mais uma questãozinha de Stokes. Vamos juntos!
Antes de mais nada, já sabe né?! Temos que enxergar o que tacontesseno:
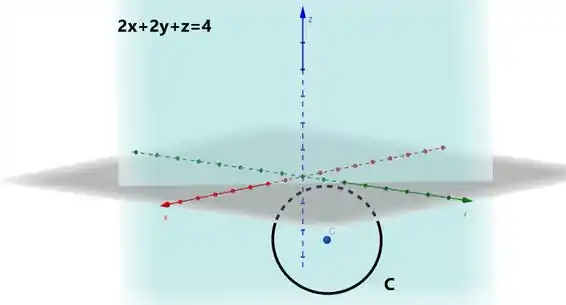
É dessa criatura aí que o enunciado ta falando. Ele diz que para um determinado raio :
E Stokes nos diz que:
Vamos tentar encontrar aquela integral dupla. Lembrando que ela é dada sob uma superfície, então não vamos mais trabalhar com a curva acima, e sim com essa superfície abaixo:
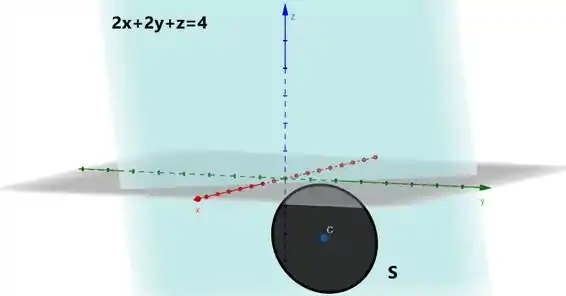
Percebe a diferença? Sim, pode dizer que a superfície é uma curva preenchida; eu deixo! Hahahaha
Passo 2
Com essa superfície em mente, podemos tentar calcular aquela integral lá. Vamos começar tentando achar o rotacional desse trem:
E o enunciado nos deu:
Só precisamos encontrar todas essas derivadas parciais aí:
E
Belezura, então o nosso rotacional é:
Agora só falta o vetor normal à essa superfície; repare que ser normal à superfície é na verdade ser normal ao plano .
Onde quer chegar com isso?? Lembra que para achar o vetor normal à qualquer plano é só pegar os valores que aparecem na frente dos , e ?
Sim, é muito tranquilo!
Nosso vetor vai ficar assim ó:
Mas por definição é um vetor unitário, então:
Lembra como se chama aquele cara ali em baixo?? É a norma do vetor, ou seja, o tamanho do vetor; então teremos:
No final das contas o que vamos jogar dentro da integral é:
Sacou a parada?
Passo 3
Então já podemos jogar tudo que encontramos dentro da integral:
Lembrando que temos um porduto escalar ali:
E finalmente:
A integral daquele cara que sobrou alí pode ser justamente a area da nossa superfície; ou seja:
Como no enunciado ele disse que:
Então,
Teje respondido então. See you...
Resposta
Ecnontramos que .