Enunciado
Cálculo - Diva Flemming - Cálculo A- Ed: 6º - Capítulo 3.6 - Ex. 8
Definir e fazer o gráfico de uma função tal que e .
Passo 1
Então galera, antes começar a resolução vale ressaltar que existem INFINITOS exemplos de funções que atendem as características dadas pelo enunciado, tudo bem? O que vamos fazer aqui é utilizar apenas uma, que já será o suficiente! A primeira característica que a função tem que ter é ter um limite resultando em quando pela direita! Em outras palavras, para temos que escrever uma função que resulte em e isso não é tão difícil de imaginar, não é mesmo? Uma função interessante seria:
Essa é a primeira característica, ok? Então vamos para a próxima!
Passo 2
A segunda característica que a função tem que ter é ter um limite resultando em quando pela esquerda! Em outras palavras, para temos que escrever uma função que resulte em e, assim como no passo anterior, isso não é tão difícil de imaginar, não é mesmo? Uma função interessante seria:
Essa descrição foi a parte analítica da coisa, tudo bem galera? Para facilitar a visualização, podemos escrever as funções assim ó:
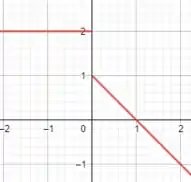
Por fim, fazendo a descrição gráfica, ou seja, plotando o gráfico dessas funções, teremos:
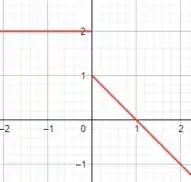
E está aí nossas descrições! 😊
Resposta
