Enunciado
Cálculo - Um curso de Cálculo Volume 2 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 8.2 - Ex. 1n
1 - Desenhe as curvas de nível e esboce o gráfico.
n -
Passo 1
Bem, sabemos que uma curva de nível pode ser encontrada fazendo . Nesse caso...
CARA! O que é isso aí? SIMMMM!
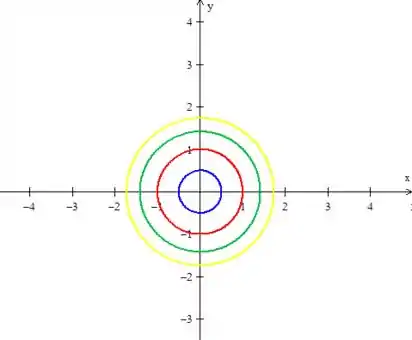
Como é sempre constante, são circunferências!
Agora, repare que deve ser , já que precisamos de um valor positivo para . Mas fora isso, para qualquer outro valor de , você vai ter uma circunferência diferente.
Vamos desenhar algumas delas aqui então:
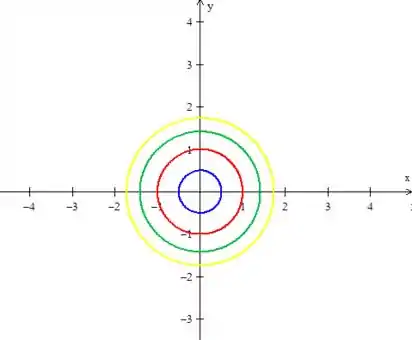
Repare o quão próximo do raio estamos! E se você almetar ainda mais, mais próximo você ficará! Mas nunca vai ser maior do que ou igual a !
Resposta
