Enunciado
Cálculo - Um curso de Cálculo Volume 2 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 8.2 - Ex. 1q
1 - Desenhe as curvas de nível e esboce o gráfico.
q -
Passo 1
Bem, sabemos que uma curva de nível pode ser encontrada fazendo . Nesse caso...
Repare que essa equação representa retas constantes e paralelas ao eixo ! Mas atenção! .
Além disso, deve estar entre e !
Vamos desenhar algumas dessas retas aqui então:
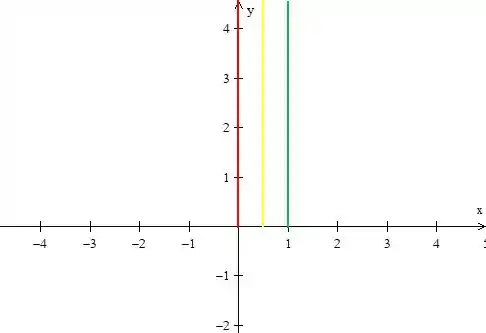
Repare que todas elas tem
Resposta
