Enunciado
Cálculo - Um curso de Cálculo Volume 2 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 8.2 - Ex. 1r
1 - Desenhe as curvas de nível e esboce o gráfico.
r -
Passo 1
Bem, sabemos que uma curva de nível pode ser encontrada fazendo . Nesse caso...
Considerando diferente de ...
Então, as curvas de níveis tem o formato de hipérboles:
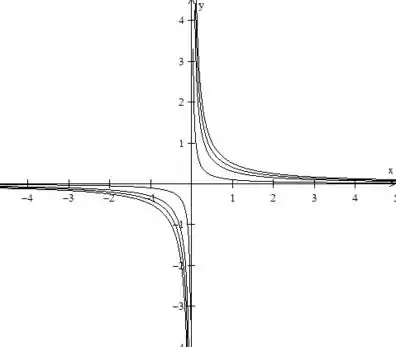
Mas só queremos o as hipérboles dentro do primeiro quadrante e ainda que tenham e (dentro desse quadrinho aqui):
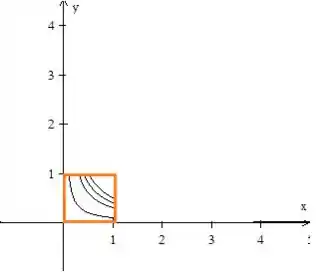
Então fica assim...
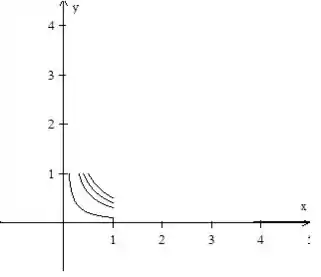
Resposta
