Enunciado

Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 14.3 - Ex. 101a

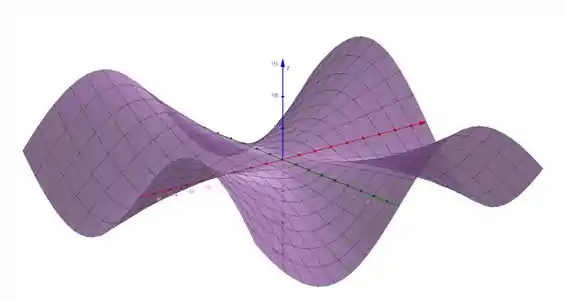
101. Seja

(a) Use um computador para traçar o gráfico de .

Passo 1

Opa, tudo jóia? A gente tem aqui uma questão de modelar um gráfico com ajudinha do computador! Já temos todos os dados necessários, mas e as ferramentas?

A ferramenta perfeita para esse caso seria o MATLAB: tem todas as funções que você pode imaginar, mas além de ser um software pago e complexo ele também não é dos mais leves...

Aí que entra o GeoGebra: gratuito, intuitivo e não precisa nem instalar pois roda no navegador.

O processo vai ser o seguinte: Pesquise por “GeoGebra” no navegador (ou vá nesse link: geogebra.org/calculator), selecione “Calculadora 3D” e insira a função no campo “Entrada”.

Passo 2

Feito isso vamos ter o seguinte gráfico:

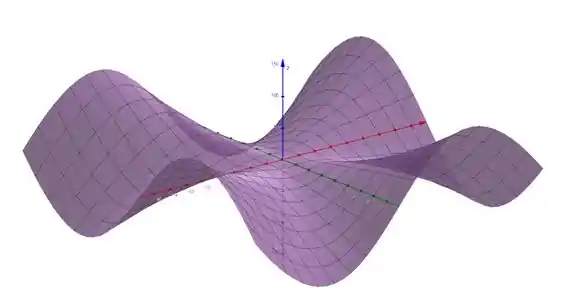
(Se o seu gráfico parece diferente tente diminuir o zoom)

Observe que no ponto da função original teríamos uma indeterminação já que estaríamos dividindo por 0, e é por isso que atribuímos um valor nesse ponto.

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Suponha que x 2 + y 2 = r 2 e x = r c o s ⁡ θ , como nas coordenadas polares. Encontre ∂ x ∂ r θ e ∂ r ∂ x y

Encontrea. ((del w)/(del x))_y b. ((del w)/(del z))_y no ponto ( x , y , z ) = ( 0,1 , pi ) sew = x^2 + y^2 + z^2 e y s e n z + z s e n x = 0

Nos Exercícios 1-3, comece desenhando um diagrama que mostreas relações entre as variáveis.Se w = x 2 + y 2 + z 2 e z = x 2 + y 2 , encontrea. ∂ w ∂ y z b. ∂ w ∂ z x c. ∂ w ∂ z y .

Encontre ( del u // del y )_x no ponto ( u , v ) = ( sqrt(2) , 1 ) , se x = u^2 + v^2 e y = u v .

Se (x, y) se move de (x0, y0) a um ponto (x0 + dx, y0 + dy) próximo, como você pode estimar a variação resultante no valor deuma função diferenciável ƒ(x, y)? Dê um exemplo.