Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 14.1 - Ex. 69
Descreva as superfícies de nível da função.
Passo 1
E aí, pessoal. Tudo certo? Vamos resolver mais uma questão.
A questão deu uma função de três variáveis e quer que a gente descreva as superfícies de nível dessa função.
Uma curva de nível é obtida quando pegamos um corte da nossa superfície numa determinada altura . Cada nível vai ter uma curva. E elas são dadas por:
Pegou a ideia? Então vem comigo!
Passo 2
Como falamos, vamos obter as curvas de nível ao fazer
As curvas de nível da função são da forma
,
com , que é uma família de cilindros circulares, com eixo principal no eixo , visto que a função não depende explicitamente de .
O raio do cilindro é , então variando aumentamos ou diminuímos a abertura do cilindro.
Para é o próprio eixo , e para não tem curva de nível.
Veja um caso de curva de nível em questão:
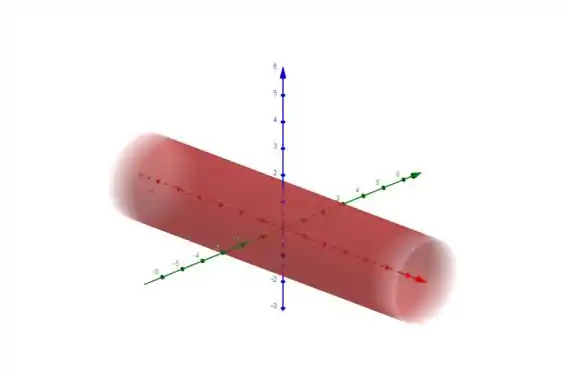
Resposta
As superfícies de nível da função são cilindros circulares cujo eixo principal é o eixo .