Enunciado
Cálculo - Um curso de Cálculo Volume 2 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 8.2 - Ex. 10 c
Seja e Desenhe de sendo
c) e
Passo 1
Vamo desenhaar?Mas já? Assim e pá?Calmaa.. Como foi dado o valor de e , bora fazer a substituição no caminho e depois aplicar na função. Então, bora!
Substituindo os valores de e , o caminho fica
Perceba que
Daí,
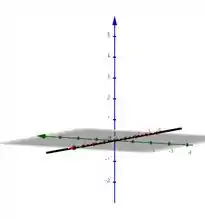
Então, agora vamos desenhar... Mas antes, se ligue numa parada: somente a coordenada tá variando e o restante é zero, então nosso desenho é essa reta.
Resposta
Exercícios de Livros Relacionados
Determine, caso existam, os valores máximo e mínimo de f em A; determine, também os ponrots em que esses valores são atingidos f x , y = x yeA = I R ² ²
Desenhe as curvas de nível e esboce o gráfico da função. f x , y = x + 1 2 + y ² + x - 1 2 + y ² ² ²
Raciocinando geometricamente, determine, caso existam, os valores máximo e mínimo de f em A, bem como os pontos em que estes valores são atingidos. f x , y = x + yeA = x , y ∈ I R 2x ≥ 0 , y ≥ 0, x +
Determine, caso existam, os valores máximo e mínimo de f em A; determine, também os ponrots em que esses valores são atingidos f x , y = x yeA = x , y ∈ I R 2 4 x 2 + y 2 = 1 ,y ≥ 0 }
Determine, caso existam, os valores máximo e mínimo de f em A; determine, também os ponrots em que esses valores são atingidos f x , y = x yeA = { ( x , y ) ∈ I R 2 | x ≥ 0ey ≥ 0 }