Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Diva Flemming - Cálculo B - Ed: 2º - Capítulo 1.4 - Ex. 7d

Desenhar as curvas de nível C k para os valores de   k dados.

d) l = 1 2 m 2 + n 2 ;         k = 0,1 , 2,3 , 4,5

Passo 1

Vamos ver como fica a equação de uma curva de nível k :

z = k

1 2 m 2 + n 2 = k

m 2 + n 2 = ( 2 k ) 2

Pronto! Agora vamos substituir o primeiro valor de k = 0 , logo

m 2 + n 2 = ( 2 × 0 ) 2

m 2 + n 2 = 0

Para k = 1 ,

m 2 + n 2 = ( 2 × 1 ) 2

m 2 + n 2 = 2 2

Para k = 2 ,

m 2 + n 2 = ( 2 × 2 ) 2

m 2 + n 2 = 4 2

Para k = 3 ,

m 2 + n 2 = ( 2 × 3 ) 2

m 2 + n 2 = 6 2

Para k = 4 ,

m 2 + n 2 = ( 2 × 4 ) 2

m 2 + n 2 = 8 2

Para k = 5 ,

m 2 + n 2 = ( 2 × 5 ) 2

m 2 + n 2 = 10 2

Agora, podemos determinar as curvas graficamente:

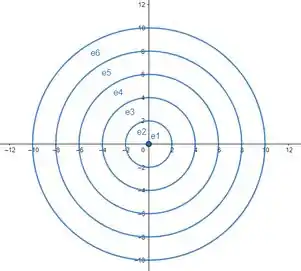
Prontinho!

Resposta

m 2 + n 2 = 0 , m 2 + n 2 = 4 , m 2 + n 2 = 16 , m 2 + n 2 = 3 6 , m 2 + n 2 = 64 , m 2 + n 2 = 100 .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Desenhar algumas curvas de nível e esboçar o gráfico:(j) z = 2 x 2 + 3 y 2
Desenhar algumas curvas de nível e esboçar o gráfico:(h) z = 8 - x 2 - y 2
Desenhar algumas curvas de nível e esboçar o gráfico:(n) z = 4 x 2 + y
Desenhar algumas curvas de nível e esboçar o gráfico:(k) z = 2 x 2 + 3 y 2
Desenhar algumas curvas de nível e esboçar o gráfico:(l) z = 4 - x 2