Enunciado
Cálculo - Diva Flemming - Cálculo B - Ed: 2º - Capítulo 1.4 - Ex. 1d
Encontrar uma função de várias variáveis que nos dê:
d) A quantidade, em metros quadrados, de papel de parede necessária para revestir as paredes laterais de um quarto retangular de metros de largura, metros de comprimento, se a altura do quarto é metros.
Passo 1
Para esse problema, lembramos que estamos falando de uma figura retangular. Como mostra a figura:
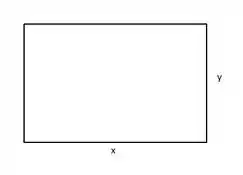
Para saber a quantidade de papel de parede, devemos calcular o perímetro de cada objeto, ou seja, a soma dos lados. No entanto, para cada variável devemos levar em consideração a altura, logo, devemos multiplicar por .
Ao nosso problema, aplicamos as variáveis (para largura), (para comprimento) e (altura). Assim, fazemos:
Prontinho!
Resposta
Exercícios de Livros Relacionados
A partir da equação dada, definir duas funções de duas variáveis, determinando seu domínio.a) y 2 = x 2 9 - x 2 + z
Determinar o domínio das seguintes funções e representa-las gráficamente:r) z = x + y - 1
Determinar o domínio das seguintes funções e representa-las gráficamente:p) f x , y , z = 1 - x 2 + 1 - y 2 - 1 - z 2
Desenhar as curvas de nível C k para os valores dek dados.a) z = x 2 - y 2 ; k = 0,1 , 2,3
Dada a função f x , y = x + y 2 x + y :a)Dar o domínio;b)Calcular f ( x + ∆ x , y ) ;c)calcular f ( - 1,0 ) ;d) Fazer um esboço do gráfico do domínio.