Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 14.1 - Ex. 48
Desenhe a curva de nível da função mostrando vários níveis.
Passo 1
A função representada possui duas variáveis, o que significa que ela existe como superfície em um espaço tridimensional. Para cada valor de e existe um .
Para a melhor compreensão desse capítulo, no entanto estamos trabalhando o comportamento dessas funções no plano .
Para encontrarmos as curvas de nível de uma função de duas variáveis, fazemos
Desse modo conseguimos avaliar o recorte da função para o valor de constante. Ou seja, no plano , para cada k escolhido teremos um nível.
Nesta questão iremos encontrar como se comporta a função para esse valor fixo e em seguida esboçar um plano contendo as curvas de nível.
Passo 2
Igualando a função dada a uma constante , temos:
Ou seja, teremos uma família de elipses cada vez maiores conforme aumenta para .
Para valores menores de e , teremos elipses cada vez menores.
Passo 3
Com posse da análise feita no passo 2, podemos traçar algumas curvas de nível, onde a cor mais escura representa níveis mais baixos da função.
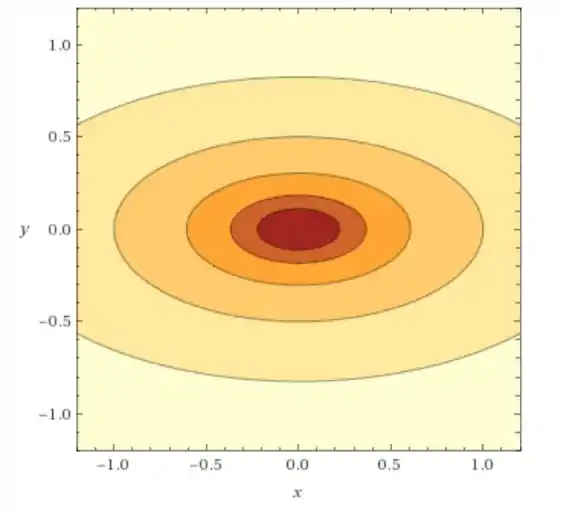
Resposta
As curvas de nível da função dada são elipses cada vez maiores, conforme k aumenta para Conforme aumenta para valores negativos, teremos elipses cada vez menores.