Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 14.1 - Ex. 80

Esboce o gráfico das funções

f x , y = x 2 + y 2

f x , y = e x 2 + y 2

f x , y = ln ⁡ x 2 + y 2

f x , y = sen ⁡ x 2 + y 2

f x , y = 1 x 2 + y 2

Em geral, se g é uma função de uma variável, como obter o gráfico de

f x , y = g x 2 + y 2

a partir do gráfico de g ?

Passo 1

Falaeee, tudo tranquilinho??? Aqui é o seguinte... o enunciado nos deu as seguintes funções:

f x , y = x 2 + y 2

f x , y = e x 2 + y 2

f x , y = ln ⁡ x 2 + y 2

f x , y = sen ⁡ x 2 + y 2

f x , y = 1 x 2 + y 2

Queremos esboçar seus gráficos utilizando uma ferramenta gráfica.

Em seguida, queremos esboçar o gráfico de f x , y tal que:

f x , y = g x 2 + y 2

Lembre-se que, em todas as funções de f a gente deve prestar bem atenção no termo x 2 + y 2 que corresponde a g x 2 + y 2 .

Mas cuidado!!! Aqui g é função apenas de x !!

Para ficar melhor de a gente entender, vamos esboçando o gráfico de f x , y em sequência com o gráfico de g x correspondente, belezinha? 😉

Passo 2

Traçando os gráficos de f ( x , y ) e g ( x ) :

Para f x , y = x 2 + y 2

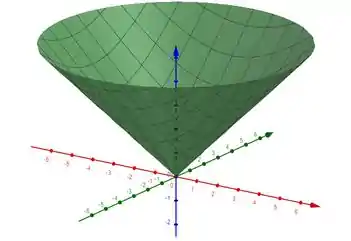
Para essa função temos que g x = x

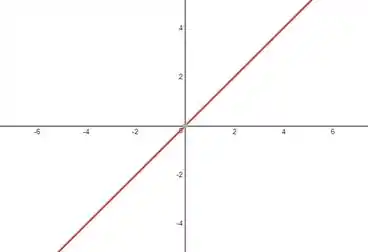
Passo 3

Para f x , y = e x 2 + y 2 :

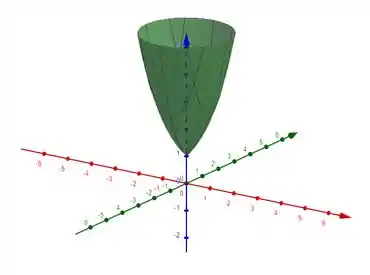
Para essa função temos que g x = e x

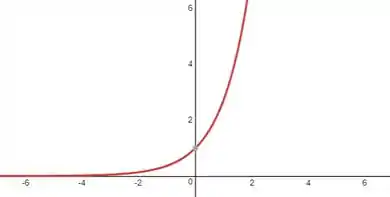
Passo 4

Para f x , y = ln ⁡ x 2 + y 2

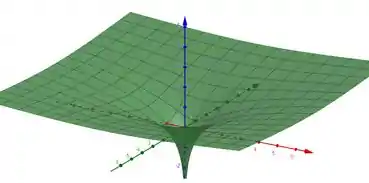
Para essa função temos que g x = ln ⁡ x

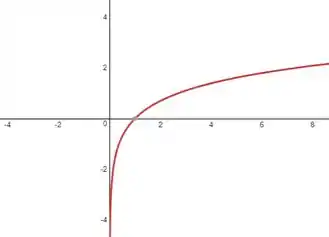
Passo 5

Para f x , y = sen ⁡ x 2 + y 2

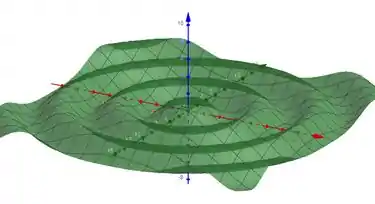
Para essa função temos que g x = sen ⁡ x

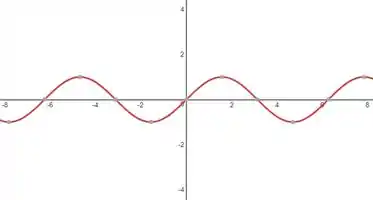
Passo 6

Para f x , y = 1 x 2 + y 2

Para essa função temos que g x = 1 x

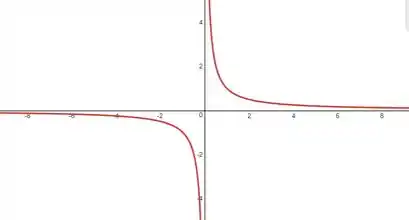
De forma geral se pegarmos a função g ( x ) com x ≥ 0 e rotacionarmos no eixo vertical, encontramos a função f x , y = g x 2 + y 2 .

Resposta

Se pegarmos a função g ( x ) com x ≥ 0 e rotacionarmos no eixo vertical, encontramos a função f x , y = g x 2 + y 2 .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Desenhe as curvas de nível e esboce o gráfico da função. f x , y = x + 1 2 + y ² + x - 1 2 + y ² ² ²
Raciocinando geometricamente, determine, caso existam, os valores máximo e mínimo de f em A, bem como os pontos em que estes valores são atingidos. f x , y = x + yeA = x , y ∈ I R 2x ≥ 0 , y ≥ 0, x +
Determine, caso existam, os valores máximo e mínimo de f em A; determine, também os ponrots em que esses valores são atingidos f x , y = x yeA = x , y ∈ I R 2 4 x 2 + y 2 = 1 ,y ≥ 0 }
Determine, caso existam, os valores máximo e mínimo de f em A; determine, também os ponrots em que esses valores são atingidos f x , y = x yeA = { ( x , y ) ∈ I R 2 | x ≥ 0ey ≥ 0 }
Determine, caso existam, os valores máximo e mínimo de f em A; determine, também os ponrots em que esses valores são atingidos f x , y = x ² x 2 + y ²eA = { ( x , y ) ∈ I R 2 | ( x , y ) ≠ ( 0,0 ) } ²