Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 14.1 - Ex. 22

Encontre e esboce o domínio da função.

f (x , y , z) = ln ( 16 - 4 x^2 - 4 y^2 - z^2 )

Passo 1

Queremos o domínio de f ( x , y , z ) . Ou seja, queremos saber os valores de x , y , z que podem ser usados para que f ( x , y , z ) seja real.

Para definir o domínio, é melhor olhar para as restrições.

Temos que:

f (x , y , z) = ln ( 16 - 4 x^2 - 4 y^2 - z^2 )

Logo,

16 - 4 x^2 - 4 y^2 - z^2 > 0

Isso implica que

4 x^2 + 4 y^2 + z^2 < 16

Dividindo tudo por 16, temos que:

(x^2)/(4) + (y^2)/(4) + (z^2)/(16) < 1

Passo 2

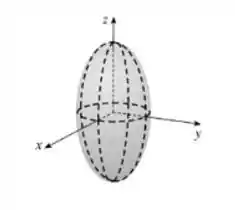
Logo, o domínio é definido por:

D : { ( x , y , z ) | (x^2)/(4) + (y^2)/(4) + (z^2)/(16) < 1 }

Trata-se dos pontos no interior do elipsoide (x^2)/(4) + (y^2)/(4) + (z^2)/(16) < 1

Resposta

D : { ( x , y , z ) | (x^2)/(4) + (y^2)/(4) + (z^2)/(16) < 1 }

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine, caso existam, os valores máximo e mínimo de f em A; determine, também os ponrots em que esses valores são atingidos f x , y = 2 - x ² + y ²eA = { ( x , y ) ∈ I R 2 ² ² }
Um ponto P descreve uma curva sobre o gráfico da função f ( x ,y )=x²+y² ² ² de modo que a sua projeção Q sobre o plano xy descreve a reta x+y=1 . Determine o ponto da curva que se encontra mais próxi
Raciocinando geometricamente, determine, caso existam, os valores máximo e mínimo de f em A , bem como os pontos em que estes valores são atingidos. f x , y = y x - 1 e A o círculo x - 3 2 + y - 1 2 ≤
Seja f x , y = x 2 x 2 + y 2 . Desenhe a imagem da curva γ t = ( x t , y t , z t ) , onde x t = Rc o s t ,y t = Rs e n t e z = f ( x , y ) (R0) . Como é o gráfico de f ?
Seja f (x , y) = x y e gamma (t) = (a t , b t , f (a t , b t)) . Desenhe de gamma sendo c) a = 1 e b = 0