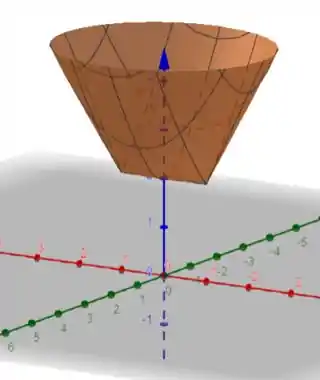
Desenhe as curvas de nível e esboce o gráfico da função.
Passo 1
Opaaa... beleza??
Nessa questão vamos primeiro desenhar as curvas de nível. Pra isso vamos chamar:
E depois vamos esboçar o gráfico.
Também vamos precisar lembrar que a fórmula da elipse é:
Onde é um ponto qualquer da elipse e e são os focos.
E que também pode ser escrita como:
Passo 2
Igualando:
Repara que temos a soma de duas raízes. Ohhh.. lembra que raiz é sempre positivo?? Então podemos dizer que é sempre maior ou igual a zero, certo?
Agora vamos pegar um pouco pesado nas lembraças de Geometria Analítica, ok? Maaas vamos devagarzinho.
Lembra que a distância entre dois pontos, e , é dada por:
Ohhh... temos coisas bem parecidas, né? Duas distâncias no lado direito da equação.
Pra primeira:
Então os pontos são e .
E pra segunda:
Então os pontos são e
Então podemos reescrever a equação lá e cima como:
Passo 3
Uaiii.. essa é bem a equação de uma elipse, né? Se a gente mudar a letra pra (só pra ficar bonitinho):
E chamar :
Ohhhh... a belíssima equação da elipse.
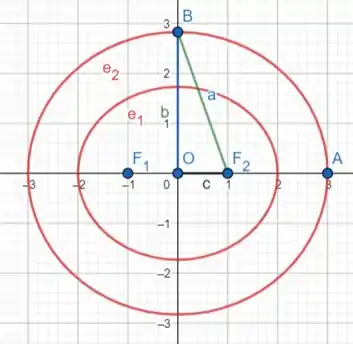
Pois muito que bem... A gente já descobriu que é uma elipse, maaas a gente não sabe se ela é deitadinha ou em pé. Se ela ta centrada no ponto (0,0) ou não...
Maaas repara que a gente tem os focos e . Se plotarmos esses pontos:
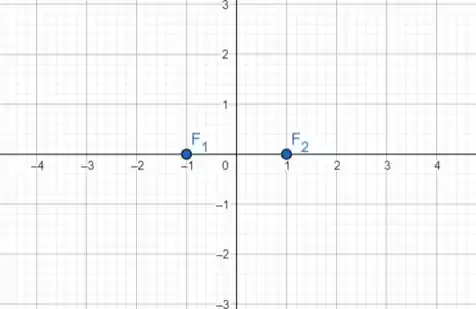
Como os focos estão no eixo , então sabemos que ela é uma elipse deitada e que está centrada no ponto .
Passo 4
Bom... agora já dá pra gente fazer um monte de curva de nível.
Como também sabemos que a equação da elipse é:
Poo... mas não temos e nem . Como vamos fazer??
A gente tem o foco que é: e .
Então temos que:
Oppa... e pra relacionar isso com e :
A gente vai atribuindo valores a e calculando os ’s. Daí é só ir desenhando no gráfico, já que é a distância de uma extremidade à outra no eixo e é a distância de uma extremidade à outra no eixo .
Pra :
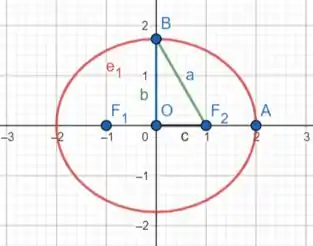
Pra :
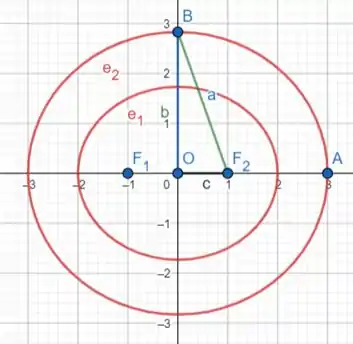
Pode até adicionar mais curvas e nem precisa de tanta exatidão, já que é só um esboço.
Passo 5
Desiste não... Bora fazer esse bendito esboço de gráfico.
Vamos testar em (que é o plano ) como a nossa função fica:
Chamando :
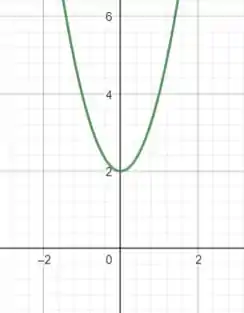
Deu uma parábola, né?? (mas suuuuper atenção porque essa parábila é só quando , ok??
E quando (que é no plano ):
E isso é uma hipérbole.
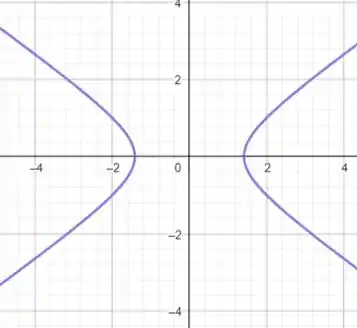
Passo 6
Temos a cara da função no eixo , que são as elipses que usamos pra fazer as curvas de nível. Temos a cara no eixo , que é a parábola. E temos a cara no eixo , que é a hipérbole.
Juntando tudo, ficamos com:
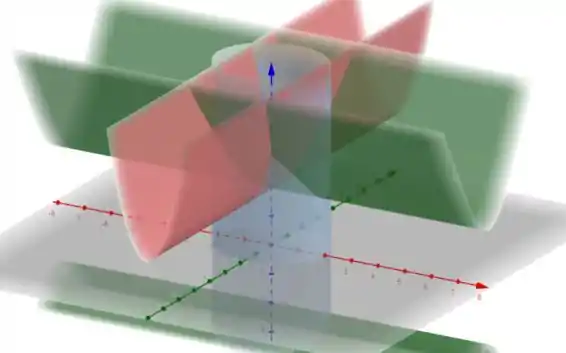
(Juuuro que se você fizer isso à mão, vai conseguir enxergar bem melhor =S)
E o gráfico fica:
Misericórdia... Acabamos essa. Vamos beber uma água é partir pra próxima??
Resposta