Determine e esboce o domínio da função.
Passo 1
Olá, meu brother. Se prepare que hoje tem aprendizado.
Dada a função:
Queremos determinar o domínio de . Ou seja, queremos saber que valores de que podem ser usados para que seja real.
Então precisamos analisar as restrições das funções para que possamos encontrar qual será o seu conjunto de valores possíveis para .
Para essa função arco seno em específico, ela é uma função inversa do seno, isso é, dado um valor de seno, ela nos dizer qual ângulo possui aquele valor.
Então para analisar essa daqui, deveremos lembrar que a função seno é limitada entre , então nossa função arco seno poderá apenas receber valores nesse intervalo.
Passo 2
A função significa “o arco, cujo seno é . Sabemos que o seno vai de a .
Logo,
Logo, o domínio é definido por
Trata-se da área entre os círculos
e
Pois precisamos estar entre esse intervalo para satisfazer a condição de existência da função.
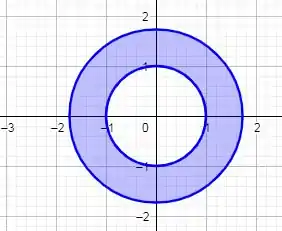
Como podemos ver no gráfico, essa região marcada em azul é o intervalo que compreende o conjunto do nosso domínio.