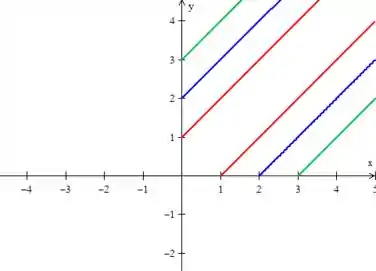
1 - Desenhe as curvas de nível e esboce o gráfico.
J -
Passo 1
Bem, sabemos que uma curva de nível pode ser encontrada fazendo . Nesse caso...
Extraindo a raiz...
Se a gente isolar em função de ...
CARA! O que é isso aí? SIMMMM!
Como é sempre constante, ambas as curvas são retas crescentes, onde uma parte de e a outra parte de (veja para ):
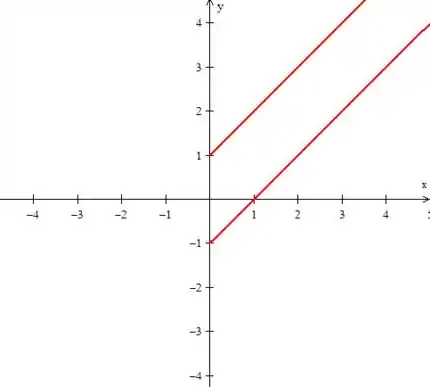
MAS CUIDADO! Essas ainda não são as curvas de níveis pedidas!
Passo 2
Repare que o problema nos deu restrições:
Isso basicamente significa que estamos restringidos apenas ao primeiro quadrante:
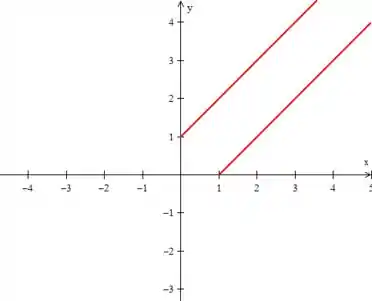
E essas sim são as curvas de nível !
Se quisermos outras curvas de níveis, tipo ou , basta desenhar retas paralelas...
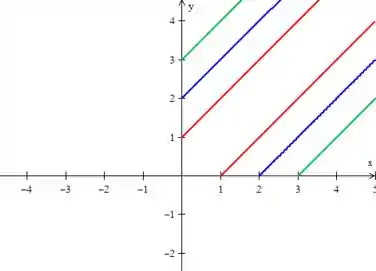
Resposta