Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Um curso de Cálculo Volume 2 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 8.2 - Ex. 4e

Determine, caso existam, os valores máximo e mínimo de f em A ; determine, também, os pontos em que estes valores são atingidos

e )   f x , y = x 2 + y 2   e   A = x , y ∈ R 2   x + 2 y = 1 } ]

(Sugestão. Observe que g y = f 1 - 2 y , y ,   y   ∈   R , fornece os valores de f sobre a reta x + 2 y = 1 . )

Passo 1

Vamos nos preocupar com a curva de nível que f forma a medida que temos que z = c

x 2 + y 2 = c

E com isso vamos determinar os valores de c m í n e c m á x de acordo com o domínio dado em A . Ao resolver o sistema em x e y onde A e f se igualam ou seja:

x + 2 y = 1 x 2 + y 2 = c

Uma forma de resolver é isolando x na primeira equação de forma que:

x = 1 - 2 y

Que é o que é sugerido na questão.

Substituindo na segunda equação teremos:

1 - 2 y 2 + y 2 = c

Isso nos deixa com

5 y 2 - 4 y + 1 = c

5 y 2 - 4 y + 1 - c = 0

Fazendo Bháskara nessa equação do segundo grau nós teremos:

y 1 ; y 2 = 4 ± 16 - 4 ⋅ 5 ⋅ ( 1 - c ) 10

y 1 ; y 2 = 4 ± - 4 + 20 c 10

Passo 2

Substituindo o valor de y 1 na equação da reta (que é A ) nós temos:

x 1 + 2 4 + - 4 + 20 c 10 = 1

x 1 + 4 + - 4 + 20 c 5 = 1

x 1 = 1 - 4 + - 4 + 20 c 5

x 1 = 1 - - 4 + 20 c 5

Analogamente substituindo y 2 = 4 - - 4 + 20 c 10 , nós teremos:

x 2 = 1 + - 4 + 20 c 5

Mas você sabe o que é o par ordenado ( x 1 ; y 1 ) e ( x 2 ; y 2 ) ? É um ponto onde as duas curvas se encontram, ou seja esses dois pares ordenados pertencem tanto a A x , y → x + 2 y = 11 e a f x , y = x 2 + y 2 , basta agora determinar para que c que isso ocorre.

Passo 3

Note que o domínio A x + 2 y = 1 não varia em relação a z ou seja para esse plano temos que a reta z = 0 é paralela a esse plano, e como f ( x , y ) é um paraboloide então temos que para um plano paralelo a z = 0 então o plano A corta f em apenas um ponto, somente existindo então um valor de c possível para que haja esse corte. Não havendo nem c m í n nem c m á x . Ou seja:

x 1 ; y 1 = x 2 ; y 2

1 - - 4 + 20 c 5 ; 4 + - 4 + 20 c 10 = 1 + - 4 + 20 c 5 ; 4 - - 4 + 20 c 10  

E essa igualdade somente existirá para c = 1 5 , pois aí teremos x 1 = x 2 e y 1 = y 2 , nos dando um ponto de encontro em:

1 5 , 2 5

Para um z em 1 5 .

Visualizando o que fizemos nós teríamos um gráfico da seguinte forma:

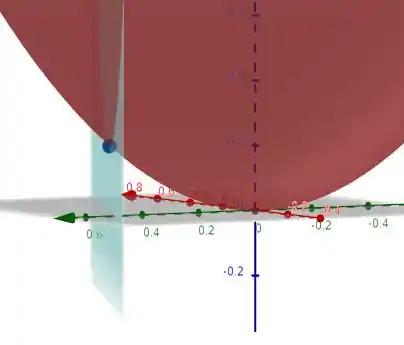
Com o plano azul sendo A . E o ponto sendo 1 5 , 2 5 , 1 5  

Resposta

Não existe máximo nem mínimo de f , apenas um ponto de encontro em:

1 5 , 2 5 , 1 5

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Descreva as superfícies de nível da função. f x , y , z = x 2 - y 2 + z 2
Esboce um mapa de contorno e um gráfico da função e compare-os. f x , y = 36 - 9 x 2 - 4 y 2
Faça um esboço do diagrama de contorno da função cujo gráfico é mostrado.
(a) Mostre que, tomando logaritmos, a função geral de Cobb-Douglas P = b L α K 1 - α pode ser expressa como ln ⁡ P K = ln ⁡ b + α ln ⁡ L K (b) Se tomarmos x = ln ⁡ L K e y = ln ⁡ P K , a equação da pa
Seja f x , y = x x 2 + y 2 . Desenhe a imagem da curva γ t = ( x t , y t , z t ) , onde x t = Rc o s t ,y t = Rs e n t e z = f ( x , y ) (R0) . Como é o gráfico de f ?