Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 14.1 - Ex. 33
Um mapa de contorno para uma função f é mostrado. Use-o para estimar os valores de e . O que você pode dizer sobre a forma do gráfico?
Passo 1
Fala ai, belezinha? Vamos entender um pouco sobre a questão, e o que devemos fazer para resolve-la?
A questão nos pede um mapa de contorno estimando os pontos dados. Para isso temos que olhar o gráfico!
Isso mesmo, apenas olhar o gráfico!
Vamos começar?
Passo 2
O que é um mapa de contorno?
É um gráfico de curvas de nível. As curvas de nível são linhas onde , onde é uma constante. Todos os pontos da linha estão na mesma altura no eixo . Os números em cima das linhas mostram o valor de .
Passo 3
Deseja-se saber o valor aproximado de .
Basta olhar no gráfico. A partir da origem, conta-se 3 quadrados para a esquerda e 3 para cima.
O ponto está entre as curvas de nível de e .
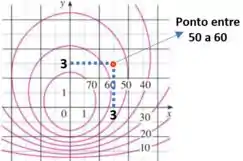
Como o ponto está mais perto da curva de , podemos estimar que .
Passo 4
Deseja-se saber o valor aproximado de .
Basta olhar no gráfico. A partir da origem, conta-se 3 quadrados para a direita e 2 para baixo.
O ponto está entre as curvas de nível de e .
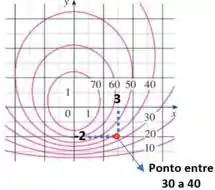
Podemos estimar que .
Passo 5
O gráfico cresce ao se aproximar da origem. Mais íngreme por baixo e gradualmente por cima.
Vale notar que quanto mais próximas estão as curvas de nível umas das outras, mais inclinado é o gráfico.
Resposta
.
.
Quanto mais próximas estão as curvas de nível umas das outras, mais inclinado é o gráfico.