Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 15.3 - Ex. 33

Utilize uma calculadora gráfica ou um computador para estimar a coordenada x do ponto de interseção y = x 4 e y = 3 x - x 2 . Se D é a região delimitada por essas duas curvas, estime

∬ D x   d A

Passo 1

E aí futuro cientista, preparado para usar todo seu talento em cálculo nessa questão de matemática? Vamos arrebentar!

Primeiro, vamos traçar as curvas y = x 4 e y = 3 x - x 2 em um gráfico, usando uma calculadora gráfica para visualizar melhor os pontos de interseção.

Depois, utilizaremos uma calculadora gráfica para esboçar as curvas y = x 4 e y = 3 x - x 2 e identificar os pontos de interseção. Em seguida, configuraremos a integral dupla para calcular o valor desejado.

O resultado da integração, que nos dará a estimativa do valor da integral dupla ∬ D x   d A .

Fazendo um esboço das curvas:

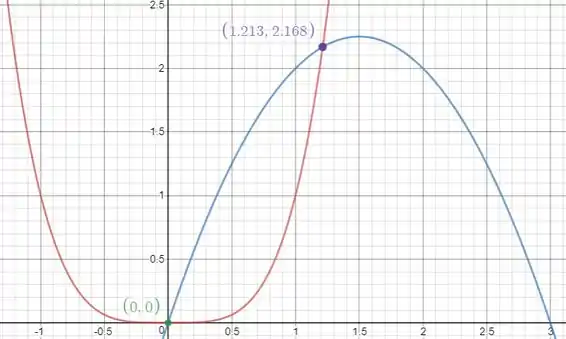
Passo 2

Após esboçar as curvas, observamos que elas se cruzam nos pontos ( 0,0 ) e ( 1,213 ;   2,168 ) . Portanto, a região D é delimitada por essas duas curvas. Agora, para calcular ∬ D x   d A , expressamos a integral como:

∬ D x   d A = ∫ 0 1,213 ∫ x 4 3 x - x 2 x   d y   d x

Passo 3

Agora, vamos resolver essa integral. Primeiro, integramos em relação a y , então e, relação a x . Isso nos dá:

∫ 0 1,213 ∫ x 4 3 x - x 2 x   d y   d x = ∫ 0 1,213 x   3 x - x 2 - x 4 d x

= ∫ 0 1,213 3 x 2 - x 3 - x 5 d x

Agora, vamos calcular essa integral. Integramos termo a termo e obtemos:

∫ 0 1,213 x   3 x - x 2 - x 4 d x = x 3 3   - x 4 4   - x 6 6 0 1,213

= 1,213 3 - 1,213 4 4 - 1,213 6 6

Com o auxílio de uma calculadora, calculamos esse valor como sendo aproximadamente 0,713 . Portanto:

∬ D x   d A   0,713

Resposta

∬ D x   d A   0,713

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine a região de integração D e troque a ordem de integração das seguintes integraisb. ∫ 0 1 ∫ - 1 - y 2 1 - y f x , y d x d y
Determine a região de integração D e troque a ordem de integração das seguintes integraisc. ∫ 0 π 2 ∫ cos ⁡ x 1 f x , y d y d x
2. AS integrais abaixo não podem ser calculadas exatamente, em termos de funções elementares, com a ordem de integração dada. Inverta a ordem de integração e faça os cálculosa. ∫ 0 1 ∫ y 1 e x 2 d x d
Utilize a transformação u = x - y ,v = x + y para avaliar ∫ ∫ R x - y x + yd A onde R é o quadrado com vértices 0 ,2 ,1 ,1 ,2 ,2 e1 ,3 .
Nos Exercícios 1-12, esboce a região delimitada pelas retas e curvas dadas. Em seguida, expresse a área da região como uma integral dupla iterada e calcule a integral. a sr e t a sy = x ,y = x 3ey = 2