Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 15.3 - Ex. 32
Determine o volume do sólido dado.
Limitado pelos cilindros e .
Passo 1
A questão pede para usarmos integrais duplas para calcular o volume entre os cilindros
Sabemos que o volume abaixo do gráfico de uma função e acima do plano é dado por
A seguir faço um plot dos dois cilindros, um com o eixo na direção e outro com o eixo na direção :
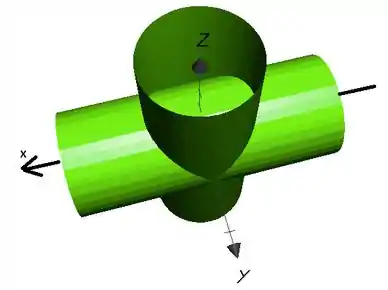
Vamos considerar a região de integração no plano limitada a
Além disso, vamos fazer apenas a integração do volume acima do plano e, daí, multiplicamos o resultado por :
A função sobre a qual vamos fazer a integral é dada pelo cilindro “deitado” na figura, cuja equação é
Para achar a fução, isolamos :
Como estamos olhando para a parte acima do plano , vamos tomar o sinal positivo:
Passo 2
Precisamos descobrir também os limites de integração. Para isso, olhamos para a região de integração no plano :
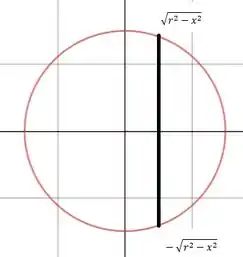
Enquanto varia de até , varia de até . Assim, a integral fica
Acontece que a integral nessa ordem é bem chata de se fazer. Por isso, vamos inverter a ordem, fazendo variar de até e variar de até . Quando fazemos isso, a integral fica
Mas por que é melhor inverter a ordem de integração? Observe que a função que vamos integrar não depende de , assim fazer a primeira integral na variável deixa tudo mais simples!
Passo 3
Antes de fazer a integral, note que ao invés de considerarmos o círculo inteiro, podemos simplesmente fazer a integral no primeiro quadrante e multiplicar o resultado por :
Isso pode ser feito por o integrando é uma função par. Como o integrando não depende de , a primeira integral é bem simples:
Na ordem de integração inversa, essa primeira integral daria bastante trabalho...
Agora ficou fácil né? Só terminar de integrar:
Assim,