Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 15.2 - Ex. 12
Desenhe um exemplo de uma região que seja:
- Tanto do tipo quanto do tipo .
- Nem do tipo nem do tipo .
Passo 1
E aí, galerinha! Como vocês estão?
Nossa questão pede que a gente traga dois desenhos, um que exemplifique uma região do tipo I e II, ao mesmo tempo e outra que não seja de nenhum dos dois tipos.
Nada melhor do que começarmos recapitulando o que são essas regiões e seus respectivos tipos:
As regiões planas das integrais duplas são os domínios de integração sobre o qual a integral é calculada. Esta região é definida pelos limites de integração para as variáveis envolvidas.
- Regiões do Tipo I: são regiões entre o gráfico de duas funções contínuas de , limitados entre dois valores fixos de no eixo , e .
- Regiões do Tipo II: são regiões entre o gráfico de duas funções contínuas de , limitados entre dois valores fixos de no eixo , e .
As duas funções devem ser contínuas e uma deve ser menor que a outra, ou seja, estar abaixo da outra no eixo , assim a região fica confinada entre e .
As duas funções devem ser contínuas e uma deve ser menor que a outra, ou seja, estar antes da outra no eixo , assim a região fica confinada entre e .
Vamos ver como ficam esses desenhos!
Passo 2
Item a:
Observe o esboço abaixo:
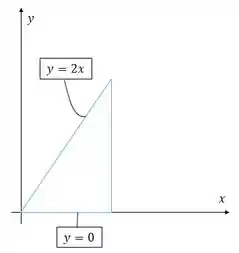
Nele podemos identificar duas funções contínuas em definindo nossa região, que é o triângulo, além de que a base do triângulo está definida entre dois valores fixos no eixo .
Agora observe o mesmo desenho:
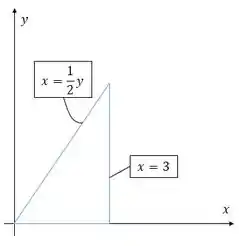
Observe que as duas funções são contínuas em . Portanto a região delimitada pelas funções é tanto do tipo quanto do tipo .
Passo 3
Item b:
Para que uma região não seja nem do tipo nem do tipo , as funções que a delimitam não podem ser contínuas nem em nem em .
Temos:
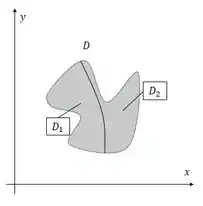
Na figura, temos que as curvas e que formam , não são funções. Podemos ver isso com o Teste da Reta Vertical: se traçarmos uma reta vertical em uma curva e a reta tocar em mais de um ponto da curva, não se trata de uma função.
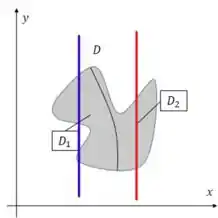
Veja como tanto a linha azul intercepta em mais de um ponto, quanto a linha vermelha intercepta em mais de um ponto. Dessa forma, nenhuma das duas curvas são funções contínuas e, portanto, não delimitam nem região do tipo I nem do tipo II.
Resposta
