Represente geometricamente o campo vetorial dado.
d)
Passo 1
Nesse caso só vamos ter campos verticais, já que cada valor de compreendido entre (por causa da condição ) associa um vetor da forma . Sendo que nesse caso o vetor vai apontar para cima, pois quando . Vamos ter um campo de vetores verticais, apontando no sentido positivo.
Eis o campo:
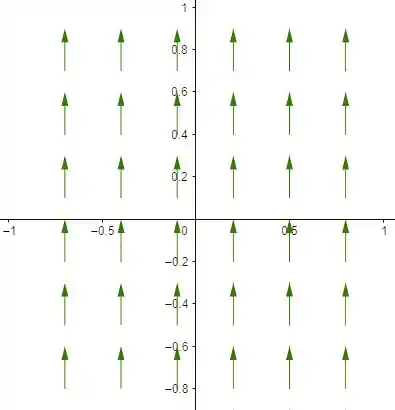
Resposta
Ei, a resposta está no passo a passo :)