Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 15.1 - Ex. 35
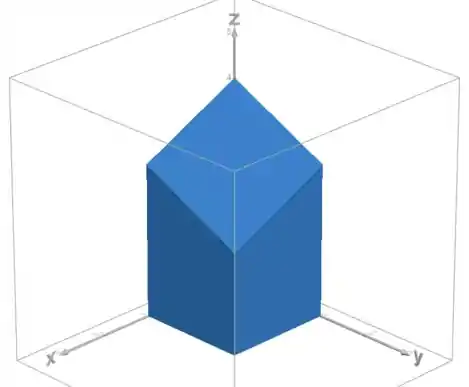
Desenhe o sólido cujo volume é dado pela integral iterada.
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
O objetivo da questão é esboçar o sólido cujo volume é especificado pela integral acima. Analisando esta integral, podemos observar que a integral dupla é definida sobre a região:
A função em questão é:
Podemos chamar de . Portanto:
Portanto, a região sólida fica abaixo do plano e acima do retângulo .
Passo 2
Para entender como fica o sólido, vamos ver como são os cortes nos planos e :
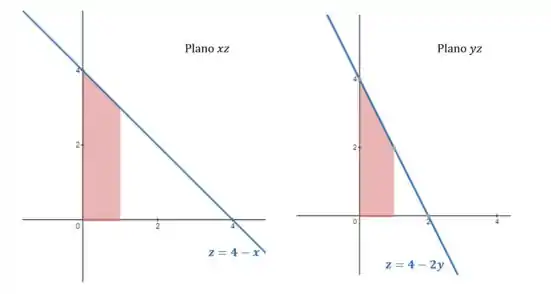
Colocando esses cortes no , conseguimos enxergar o sólido:
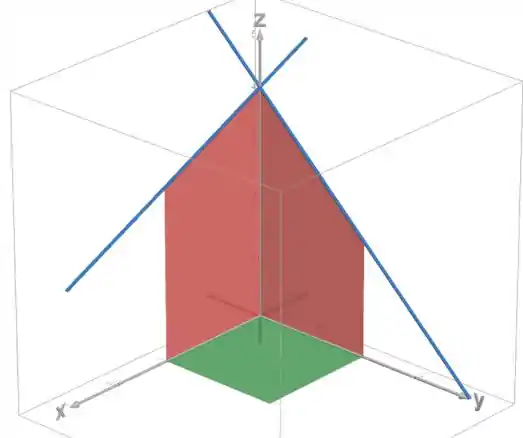
O quadrado verde é o domínio da integral .
Assim, o gráfico do sólido é mostrado na figura abaixo:
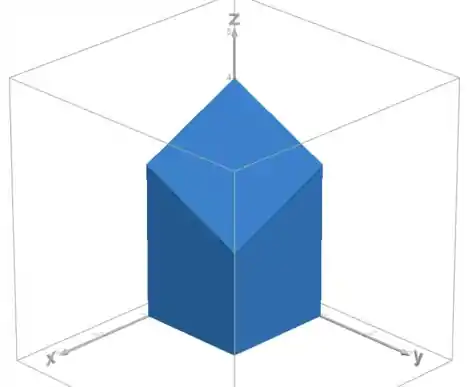
Resposta
Exercícios de Livros Relacionados
Calcular o volume da parte da esfera x 2 + y 2 + z 2 = 9 , que está entre os planos z = 0 e z = 2 .
A integral iterada representa o volume de um sólido. Descrever o sólido. ∫ 0 1 ∫ 0 2 d x d y
A integral iterada representa o volume de um sólido. Descrever o sólido. ∫ 0 2 ∫ 0 3 - 3 2 x 1 - 1 2 x - 1 3 y d y d x
A integral iterada representa o volume de um sólido. Descrever o sólido. ∫ 0 4 ∫ - 2 2 4 - x 2 d x d y
Calcule o volume do conjunto dado.{ (x , y , z) in R^3 | 0 = x = 1 , 0 = y = 1 , x^2 + y^2 = z = 2 }