Enunciado
Cálculo - Diva Flemming - Cálculo B - Ed: 2º - Capítulo 1.4 - Ex. 4k
Determinar o domínio das seguintes funções e representa-las gráficamente:
k)
Passo 1
O domínio é o conjunto no qual podemos realizar as operações com sentido. Isto é, sem divisão por zero, raízes com números negativos, logaritmos com logaritmando negativo.
Como para qualquer , temos que o domínio da função dada é todo espaço .
Sabemos que o denominador da fração deve ser diferente de 0, logo
Então, o nosso domínio é: .
Passo 2
A representação gráfica é:
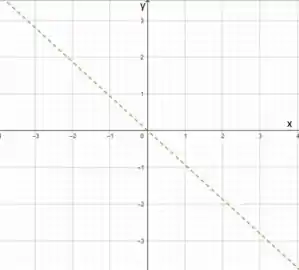
Prontinho!
Resposta
Domínio: .
Exercícios de Livros Relacionados
Dada a função f x , y = 1 x 2 + y 2 , pede-se:A equação e o esboço da curva de nivel que contém o ponto ( 0,2 ) .
Dada a função f x , y = 1 x 2 + y 2 , pede-se:As equações das curvas de nível z = 1 4 , z = 4 e z = 9 .
Considere a superficie S , união de S 1 e S 2 , onde S 1 tem equação x 2 + y 2 = 4 com 0 ≤ z ≤ 2 , e S 2 é o gráfico da função z = x 2 + y 2 definida no conjunto D , onde D = x , y ∈ R 2 4 ≤ x 2 + y 2
10- Considerando a função z = f x ,y = 7 - x 2 + y 2 ,0 ≤ x 2 + y 2 ≤ 16 , 25 - x 2 - y 2 ,16 ≤ x 2 + y 2 ≤ 25 b)Identifique a curva de nível que contém o pontoP 0 = ( 1 ,3 ) .
Nos Exercícios 1-4, determine os valores de função específicos.