Enunciado
Cálculo - Diomara - Cálculo Diferencial e Integral de Funções de Várias Variáveis- Ed: 3º - Capítulo 3.2 - Ex. 2c
Considere a superficie , união de e , onde tem equação com , e é o gráfico da função definida no conjunto , onde
Passo 1
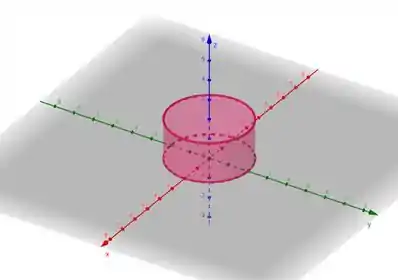
Bom galera, a gente precisa esboçar e sabemos que ela é a união de com , primeiro temos que identificar cada parte, começando por :
Isso é a equação de uma circunferência de raio e é dito que se extende pelo eixo em , logo temos um cilindro assim:
Passo 2
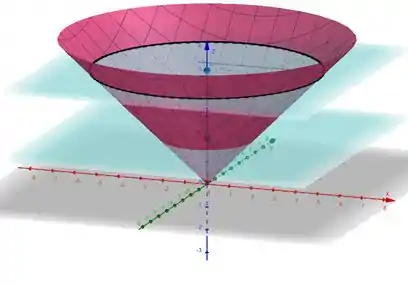
Belezinha, agora é dado por:
Que é a equação de um cone no eixo , mas ela possui a restrição:
Que na forma pratica quer dizer apenas que o raio serve para gente apenas a parte que possui raio maior que e menor que em relação ao eixo , ou seja, temos a superficie do cone entre os planos:
Passo 3
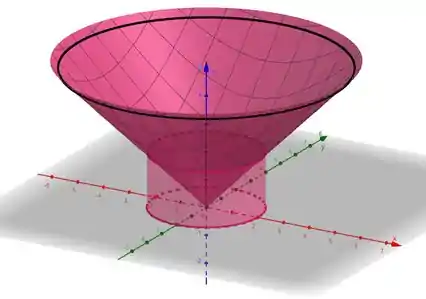
Por fim, a união dos dois fica:
Resposta
Exercícios de Livros Relacionados
Identificar as afirmações verdadeiras:h) O conjunto x ,y ∈ R 2 x ,y ∈ Q } não tem ponto de acumulação.
Verificar se o conjunto A = {(x , y) in R^2,x , y in N} tem ponto de acumulação.
Identificar as afirmações verdadeiras:j) Se A é um conjunto aberto, nenhum ponto da fronteira de A pertence a A .
Identificar as afirmações verdadeiras:i) Todos os pontos de um conjunto aberto A são pontos de acumulação de A .
Identificar as afirmações verdadeiras:a) A união de bolas abertas é um conjunto conexo.