Enunciado
Cálculo - Diomara - Cálculo Diferencial e Integral de Funções de Várias Variáveis- Ed: 3º - Capítulo 5.4 - Ex. 5a
Determine a área da região limitada pelas curvas:
e .
Passo 1
E aí, galerinha!! Vamos lá com mais um exercício com o Responde Aí!! :D
Sabemos que a integral dupla representa geometricamente o volume de uma região no espaço. Então, como a área possui uma dimensão a menos que o volume, ela pode ser representada por uma única integral simples:
Assim, com as curvas dadas no enunciado, podemos determinar os limites de integração e a função de que representa a região.
Passo 2
Dessa forma, a primeira coisa a se fazer é o esboço da nossa região que é dada por:
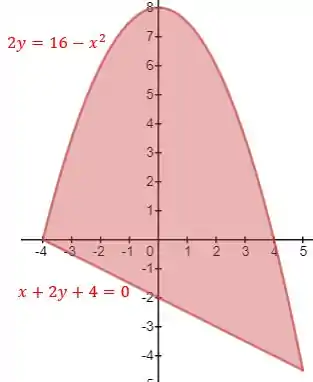
Podemos perceber que ela possui uma mudança de forma no eixo (uma parábola acima e aproximadamente um triângulo abaixo do eixo). Então, iremos separá-la em duas regiões diferentes, sendo que a área de cada uma será representa por integrais diferentes.
O próximo passo é definir a função de cada curva. Então, dizendo que a região acima do eixo é a região , a sua curva é dada por:
Já a curva da região (região de baixo) é dada por:
Passo 3
Para determinarmos o intervalo de integração podemos utilizar as equações das curvas de cada região e igualar ambas:
Tal que, passando todos os termos para um lado da equação apenas:
Multiplicando tudo por :
Essa equação e segundo grau nos dá as raízes de que, no nosso caso, são os limites de integração. Então, através da fórmula de Bhaskara:
Logo:
Passo 4
Portanto, podemos agora calcular a integral da região de cima que será dada por:
Então, resolvendo-a:
E substituindo os intervalos de integração:
Logo:
Passo 5
Já para a região de baixo, sua área será dada por:
Percebeu que o sinal da curva não é o mesmo? Isso se dá porque a integral representa a área abaixo de uma curva. Como no nosso caso queremos a área acima dela, precisamos inverter o sinal da função.
Então, resolvendo-a:
E substituindo os intervalos de integração:
Logo:
Passo 6
Por fim, sabemos que a nossa região é dada pela interseção dessas duas regiões que consideramos. Então, a área total é a soma das áreas de cada região, ou seja:
Portanto:
Encontrando o MMC: