Enunciado
Cálculo - Diomara - Cálculo Diferencial e Integral de Funções de Várias Variáveis- Ed: 3º - Capítulo 5.4 - Ex. 2a
2. AS integrais abaixo não podem ser calculadas exatamente, em termos de funções elementares, com a ordem de integração dada. Inverta a ordem de integração e faça os cálculos
a.
Passo 1
Oii, estamos agora embarcando no mundo das integrais. Como você muito bem sabe, uma interpretação geométrica de integrais é o cálculo de áreas. Assim os intervalos de integração nos dizem que região do Plano estamos. E olha que bacana! Não importa a ordem de integração o valor final SEMPRE tem que ser o mesmo. Assim podemos fazer um integral moleza se nós manipularmos quais variáveis vamos integrar primeiro, pense sempre em poupar esforço!
Passo 2
No nosso caso temos essa integração
Essa função só pode ser resolvida pode series de potência, que é o escopo de cálculo 4. Ainda somos meros mortais em cálculo 2, então precisamos de uns truques para fugir dessas integrações mais bizarrinhas. Primeiro vamos descobrir a região de integração
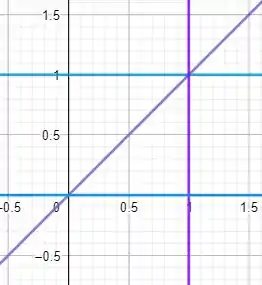
Nossa região é a interseção entre as retas. Opa! Ficou confuso. Qual é a parte. De cima ou de baixo? Temos que lembrar que lemos x da esquerda para a direita. E y de cima para baixo. Assim x começa na reta e termina na reta . Com isso podemos afirmar que nossa região é
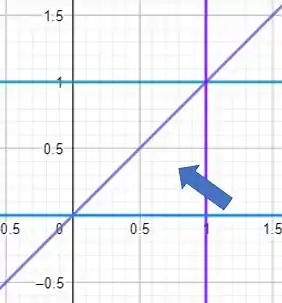
Com isso nossa nova ordem de integração pode ser
Passo 3
Vamos integrar agora
Essas integrais que têm exponencial podemos fazer por vários meios diferentes. Um que eu acho muito pratico é fazer o seguinte : pregar a exponencial e derivar e ver o que acontece
Logo podemos ver que é uma derivada de apenas ajustando um fator. Logo podemos dizer que
Terminamos por aqui. Pode comemorar! \o/
Te vejo na próxima resolução
: )