Enunciado
Cálculo - Diomara - Cálculo Diferencial e Integral de Funções de Várias Variáveis- Ed: 3º - Capítulo 4.2 - Ex. 5
5. De uma longa folha de alumínio com 12 cm de largura, deseja-se construir uma calha , dobrando-se os lados da folha para cima e formando duas abas de mesmo tamanho , de modo que essas abas façam o mesmo ângulo com a horizontal . Qual a largura das abas e que ângulo elas devem fazer com a horizontal a fim de que a capacidade de cada calha seja máxima ?
Passo 1
Por mais que pareça estranho nesse enunciado. A calha tem o seguinte formato
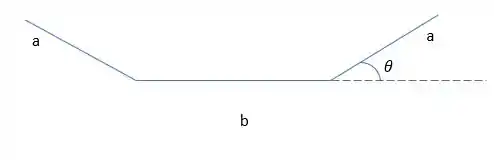
Temos então em mãos as seguintes equações
A area podemos usar relações de triângulos para poder concluir que
Passo 2
O que vamos fazer agora é derivar A em função de a. E como é uma otimização vamos igualar a zero
Entao
Ou
Se o ângulo for zero, não temos solução. Então só nos resta a segunda opção
Como temos a relação de perímetro la em cima podemos dizer que
Passo 3
Vamos agora substituir esse valor de a na nossa area e derivar em relação ao ângulo e novamente igualar a zero
Com isso nossa derivada será
Passo 4
Vamos descobrir a com isso
Terminamos por aqui. Pode comemorar! \o/
Te vejo na próxima resolução
: )