Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 16.6 - Ex. 44

Determine a área da superfície.

A parte da superfície z = 1 + 3 x + 3 y 2 que está acima do triângulo com vértices 0,0 , 0,1 e 2,1

Passo 1

Fala ai galera, o exercicio pede para calcularmos a área da superfície z = 1 + 3 x + 3 y 2 que está acima do triângulo com vértices 0,0 , 0,1 e 2,1 .

Para calcular a área iremos utilizar a fórmula:

A S = ∬ D 1 + ∂ z ∂ x 2 + ∂ z ∂ y 2 d A

Então primeiro iremos achar as derivadas parciais ∂ z ∂ x e ∂ z ∂ y e substituir na integral.

Depois iremos precisar achar os limites de integração, ou seja, quanto x e y variam e aí é só substituir tudo na integral e fazer o cálculo, beleza?

Vamos nessa!!!

Passo 2

Vamos começar pelas derivadas parciais. Sabendo que:

z = 1 + 3 x + 3 y 2

Logo:

∂ z ∂ x = ∂ 1 + 3 x + 3 y 2 ∂ x = 3

∂ z ∂ y = ∂ 1 + 3 x + 3 y 2 ∂ y = 6 y

Substituindo na integral:

A S = ∬ D 1 + 3 2 + 6 y 2 d A

Passo 3

Belezinha galera, sabemos que como d A é a área logo podemos escrevê-la sendo:

d A = d x d y

Agora vamos achar os limites de integração, a função que tem tanto x   quando y

é encontrada ao olharmos para o triângulo.

Sabemos agora que a superfície está acima do triângulo que possui os pontos:

0,0 , 0,1 e 2,1

Graficamente: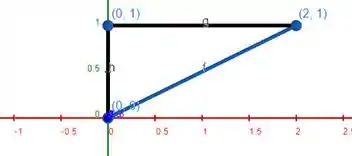

Para achar os limites precisamos saber quem é essa reta azul, beleza?

Conseguimos achar a equação da reta através de dois pontos, que é o que temos. Logo:

Com os pontos 0,0 e 2,1 é:

y = a x + b

Para 0,0

0 = a . 0 + b

b = 0

Para 2,1

1 = a . 2

a = 1 2

Logo nossa equação da reta é:

y = 1 2 x

Escrevendo em função de x :

x = 2 y

Que nos dá:

0 ≤ y ≤ 1 ,   0 ≤ x ≤ 2 y

Pronto, é só agora substituir na integral:

A S = ∬ D 1 + ∂ z ∂ x 2 + ∂ z ∂ y 2 d A

∫ 0 1 ∫ 0 2 y 1 + 3 2 + 6 y 2 d x d y

Passo 4

Agora só partir para resolução. Começando por:

∫ 0 2 y 1 + 3 2 + 6 y 2 d x

Como tudo é constante em relação a x logo:

1 + 3 2 + 6 y 2 ∫ 0 2 y d x

Assim:

10 + 36 y 2   x 0 2 y

10 + 36 y 2   2 y - 0

Logo:

∫ 0 2 y 1 + 3 2 + 6 y 2 d x = 2 y 10 + 36 y 2

Substituindo em:

∫ 0 1 ∫ 0 2 y 1 + 3 2 + 6 y 2 d x d y

∫ 0 1 2 y 10 + 36 y 2   d y

Passo 5

Beleza, vamos resolver agora:

∫ 0 1 2 y 10 + 36 y 2   d y

Vamos fazer por substituição:

10 + 36 y 2 = u

d y   u ' = d u

d y   ( 72 y ) = d u

d y   = d u 72 y  

Substituindo:

∫ 0 1 2 y u   d u 72 y  

Cortando os valores iguais e passando a constante para fora:

1 36   ∫ 0 1 u   d u

1 36     2 3   u 3 2 0 2 y

Substituindo 10 + 36 y 2 = u

1 36     2 3   ( 10 + 36 y 2 ) 3 2 0 1

Passando a constante para fora e substituindo os limites de integração:

1 54     ( 10 + 36 ( 1 ) 2 ) 3 2 - ( 10 + 36 ( 0 ) 2 ) 3 2

1 54     ( 10 + 36 ) 3 2 - ( 10 ) 3 2

Assim:

∫ 0 1 2 y 10 + 36 y 2   d y = 1 54 46 3 2 - 10 3 2

Logo:

A S = 1 54 46 3 2 - 10 3 2

Resposta

A S = 1 54 46 3 2 - 10 3 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

∬_S (x^2 + y^2) d S , onde S é a esfera x^2 + y^2 + z^2 = a^2 .
Seja S a superfície obtida girando-se a curva plana z = 1 - x 2 , 0 ≤ x ≤ 1 em torno do eixo z . Calcule ∬ S 1 | x y | x 2 + y 2 d s , onde S 1 é a porção de S que se encontra no interior do cilindro
Sabendo-se que o centro de massa ( x c , u c , z c ) de uma superfície S é definido por x c = ∬ S x f x , y , x d s M , y c = ∬ S y f x , y , x d s M e z c = ∬ S z f x , y , x d s M ,onde M é a massa
Sabendo-se que o centro de massa ( x c , u c , z c ) de uma superfície S é definido por x c = ∬ S x f x , y , x d s M , y c = ∬ S y f x , y , x d s M e z c = ∬ S z f x , y , x d s M ,onde M é a massa
Seja S uma superfície fechada tal que S = S 1 ∪ S 2 , onde S 1 e S 2 são as superfícies de revolução obtidas pela rotação em torno do eixo z das curvas C 1 : z = 1 - x , 0 ≤ x ≤ 1 e C 2 : z = 0 , 0 ≤