Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Diomara - Cálculo Diferencial e Integral de Funções de Várias Variáveis- Ed: 3º - Capítulo 7.6 - Ex. 2

Seja S a superfície obtida girando-se a curva plana z = 1 - x 2 , 0 ≤ x ≤ 1 em torno do eixo z . Calcule ∬ S 1 | x y | x 2 + y 2 d s , onde S 1 é a porção de S que se encontra no interior do cilindro x 2 + y 2 = y .

Passo 1

Galera, vamos olhar em torno do eixo z :

z = 1 - x 2

com intervalo de 0 ≤ x ≤ 1 .

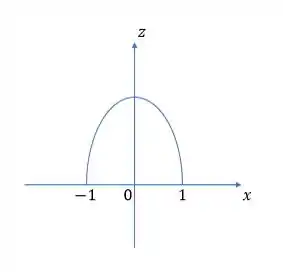
S : z = 1 - x 2 + y 2 , com x 2 + y 2 ≤ 1 .

A área S 1 que queremos, é a porção S da parte de dentro do cilindro:

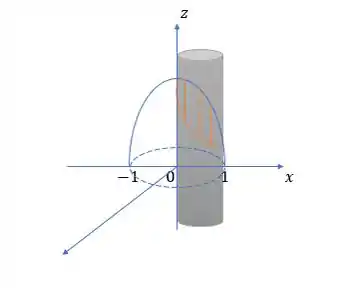
S 1 :     x 2 + y 2 e portanto x 2 + ( y - 1 / 2 ) ² = 1 / 4

Agora, vamos parametrizr S 1 :

x , y = x , y , 1 - x 2 - y 2

E então,

D 1 : x , y x 2 + y 2 ≤ y .

Nós temos que f x , y = 1 - x 2 - y 2 .

Passo 2

Para encontrarmos d s fazemos:

d s = ∂ f ∂ x 2 + ∂ f ∂ y 2 + 1   d x d y = 4 x 2 + 4 y 2 + 1   d x d y = 1 + 4 x 2 + y 2   d x d y .

A área de S 1 então:

A S 1 = ∬ S 1 | x y | x 2 + y 2 d s = ∬ D 1 x y x 2 + y 2 ⋅ 1 + 4 x 2 + y 2   d x d y

Note que precisamos fazer uma mudança para coordenadas polares.

Recordando:

x = r cos ⁡ θ

y = r   s e n   θ

y = r

Logo,

x 2 + y 2 = y

⇒ r 2 cos 2 ⁡ θ + r 2 s e n 2 θ = r   s e n   θ

⇒ r 2 = r   s e n   θ

⇒ r = s e n   θ

Então, nosso novo intervalo de integração é:

0 ≤ θ ≤ π

Passo 3

E nossa nova integral é

∫ 0 π ∫ 0 s e n   θ r 2 | s e n   θ ⋅ cos ⁡ θ | r 2 ⋅ 1 + 4 r 2 ⋅ r   d r   d θ = ∫ 0 π ∫ 0 s e n   θ r 2 | s e n   θ ⋅ cos ⁡ θ | r 2 ⋅ 1 + 4 r 2 ⋅ r   d r   d θ - ∫ π 2 π ∫ 0 s e n   θ r   s e n θ cos ⁡ θ ⋅ 1 + 4 r 2   d r   d θ

Resolvendo a integral de dentro:

1 8 ⋅ 2 3 ∫ 0 π 2 s e n   θ cos ⁡ θ   1 + 4 r 2 3 2 0 s e n   θ d θ - 1 8 ⋅ 2 3 ∫ π 2 π s e n θ cos ⁡ θ 1 + 4 r 2 3 2   d θ 0 s e n   θ = 1 12 ∫ 0 π 2 s e n θ cos ⁡ θ   1 + 4   s e n 2   θ 3 2 - 1   d θ - 1 12 ∫ π 2 π s e n   θ cos ⁡ θ   1 + 4   s e n 2 θ 3 2 - 1     d θ

Para continuar, precisamos fazer uma substituição:

u = 1 + 4   s e n 2   θ

d u = 8   s e n θ cos ⁡ θ   d θ

= 1 12 ⋅ 1 8 ∫ 0 π ( u 3 2 - 1 )   d u - 1 12 ⋅ 1 8 ∫ π 2 π u 3 2 - 1 d u = 1 96 2 5 ⋅ 1 + 4   s e n 2 θ 5 2 - 1 + 4   s e n 2   θ 0 π 2 - 1 96 [ 2 5 1 + 4   s e n 1 θ ) 5 2 - 1 + 4   s e n 2   θ π 2 π = 1 96 2 5 ⋅ 25 5 - 5 - 2 5 + 1 - 1 96 2 5 - 1 - 2 5 ⋅ 25 5 + 5 = 1 96 ⋅ 2 5 ⋅ 25 5 - 1 96 ⋅ 22 5 + 1 96 ⋅ 2 5 ⋅ 25 5 = 2 96 ⋅ 2 5 ⋅ 25 5 - 2 96 ⋅ 22 5 = 25 5 - 11 120

Resposta

25 5 - 11 120

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule ∬ K f x , y , z d S sendo: f x , y , z = x ;σ u , v = u ,v ,u 2 + v ,0 ≤ u ≤ 1eu 2 ≤ v ≤ 1 .
Calcule ∬ K f x , y , z d S sendo: g )f x , y , z = z ;σ é a parte da superfície z 2 = x 2 + y 2 que se encontra acima do paraboloide 4 z = x 2 + y 2 + 3 .
Calcule ∬ K f x , y , z d S sendo: i )f x , y , z = 1 - x 2 ;σ é a parte da superfície cilíndrica z 2 + x 2 = 1 que se encontra dentro do cone z ≥ x 2 + y 2 .
Calcule ∬ K f x , y , z d S sendo: i )f x , y , z = z 1 + 4 x 2 + 4 y 2 ;σ é a parte do paraboloide z = 1 - x 2 - y 2 que se encontra dentro do cilindro x 2 + y 2 ≤ 2 y .
Calcule ∬ K f x , y , z d S sendo: c )f x , y , z = x 2 + y 2 ;σ u , v = u , v ,u 2 + v 2 ,u 2 + v 2 ≤ 1 .