Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 16.3 - Ex. 32
Determine se o conjunto dado é ou não: (a) aberto, (b) conexo por caminhos e (c) simplesmente conexo.
Passo 1
Olá, tudo bem?
Vamos analisar o que a questão está querendo.
Ela quer que a gente diga se a região onde o módulo de varia entre e , sem nunca assumir esses valores, e podendo ser qualquer valor, é aberta, conexa por caminhos ou simplesmente conexa.
Primeiro, quando temos o módulo de limitado por dois valores
isso significa que ele varia assim:
E
Então, para
Temos que
e
Ok. Mas o que são essas classificações?
Uma região aberta significa que precisamos ser capazes de andar infinitamente dentro dela para todos os lados sem sair dela. Normalmente isso ocorre quando os extremos não estão incluídos ou algum ponto está faltando.
Uma região conexa por caminhos significa que precisamos conseguir ir de um lugar para o outro sem sair dela.
Exemplo de uma região conexa por caminhos:
Exemplo de uma região não conexa por caminho:
Uma região simplesmente conexa significa temos que ser capazes de ir para qualquer lugar dessa região por qualquer caminho e sem sair dela. Ou seja, a região não pode ter buracos!
Exemplo de uma região simplesmente conexa:
Exemplo de uma região não simplesmente conexa:
Portanto, primeiro vamos desenhar a região
e depois vamos analisar se ela se encaixa em cada uma dessas classificações.
Vamos lá?
Passo 2
Vamos desenhar a região formada por
E como vimos no passo 1, isso quer dizer que estamos usando as coordenadas , sendo que o está limitado por
e o não
A região desenhada fica assim:
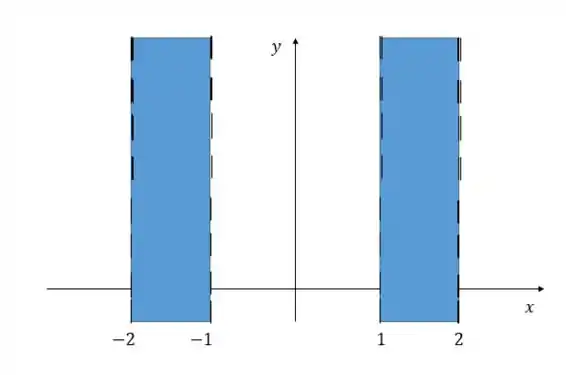
Não incluindo os valores extremos que são , , e , pois os intervalos são abertos!
E essas barras se estendem infinitamente para cima e para baixo, pois não possui restrições!
Passo 3
Vamos analisar essa região para saber que ela é aberta. Letra a.
Vamos imaginar que estamos dentro dessas barras azuis e querermos sair delas.
Se andarmos apenas na direção , nunca sairemos, pois é infinito.
Se andarmos na direção , poderemos chegar muito perto de sair, mas nunca sairemos, pois precisamos chegar nos pontos extremos e eles não estão incluídos nessa região.
Logo, nunca conseguiremos sair dessas barras azuis.
Assim, a região é aberta, pois por mais que tentemos, nunca sairemos.
Passo 4
Agora, queremos saber se ela é conexa por caminhos. Letra b.
Novamente, vamos nos imaginar dentro de uma dessas barras.
Podemos ir para qualquer lugar dentro dela, certo? Mas e se a gente quiser ir para a outra barra?
Teremos um problema, precisaremos passar pela região branca para fazer isso!
Se isso acontece, essa região não é conectada por caminhos, então ela não é conexa por caminhos!
Passo 5
Vamos ver se ela é simplesmente conexa. Letra c.
Aqui, se a região não é conexa por caminhos, ela nunca poderá ser simplesmente conexa.
Basicamente falando, uma região simplesmente conexa não pode ter buracos!
Resposta
A região
é
- Aberta
- Não conexa por caminhos
- Não simplesmente conexa