Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 14.1 - Ex. 18
Determine e esboce o domínio da função.
Passo 1
Olá, meu brother. Se prepare que hoje tem aprendizado.
Dada a função:
Queremos determinar o domínio de . Ou seja, queremos saber que valores de que podem ser usados para que seja real. Para definir o domínio, é melhor olhar para as restrições das funções. A restrição de uma função raiz quadrada, é que não podemos ter valores negativos dentro da raiz, então é isso que iremos analisar aqui.
Como temos duas raízes, deveremos analisar então qual o intervalo para a primeira raiz e o intervalo para a segunda raiz, e então unir esses intervalos.
Passo 2
Para definir o domínio, é melhor olhar para as restrições:
Temos duas restrições aqui (uma para cada raiz):
1.
2.
Passo 3
Logo, o domínio é definido por
Vale notar que a equação representa o círculo centrado em e de raio . Porém, como , o domínio representa o semicírculo superior.
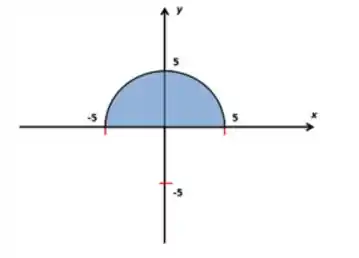
Então o que temos no gráfico, é a região do nosso domínio, nosso domínio está dentro da região azul, que foi gerada a partir da intersecção dos domínios das duas raízes.