Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 14.3 - Ex. 13
Determine e e faça os gráficos com domínios e pontos de vista que lhe permitam ver a relação entre eles.
Passo 1
Vamos lá! Vou te ajudar a resolver essa atividade hoje.
Dada a função de duas variáveis:
Deveremos encontrar as derivadas parciais:
Fazemos isso derivando em relação a variável dada e considerando as outras variáveis como constantes.
Em relação aos gráficos iremos utilizar um software gráfico para gerar e podermos visualizar os gráficos e seus comportamentos.
Passo 2
Pra fazer a derivada parcial a gente deriva o e considera o como uma constante. Aí vai ficar:
Só isso!
Pra fazer a derivada parcial é só fazer o contrário: derivamos o e consideramos o constante:
Prontinho! Só jogar isso num programa pra gerar os gráficos agora.
Passo 3
Os gráficos, para :
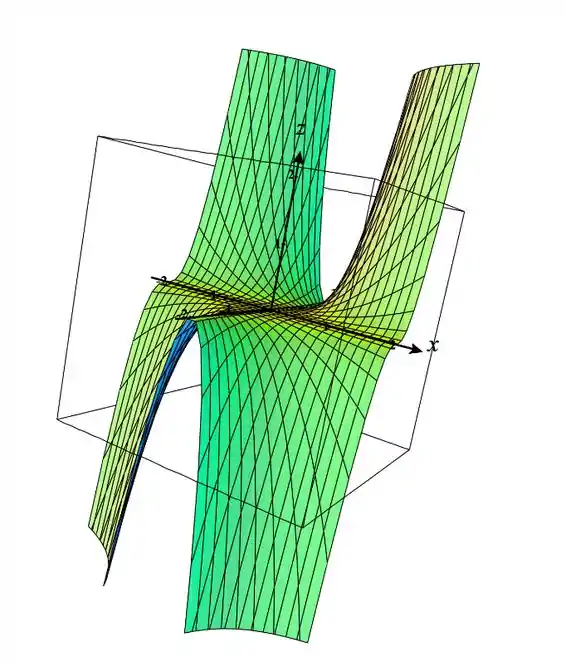
Agora para
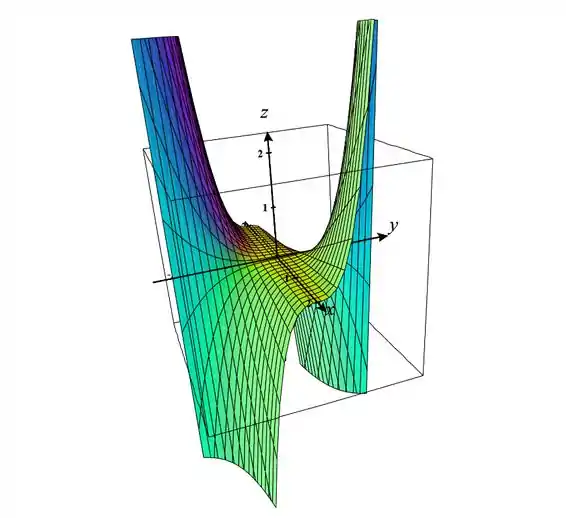
E por último :
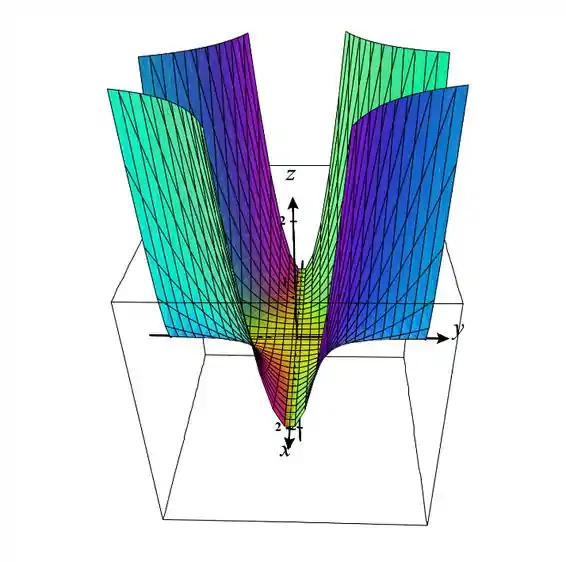
Veja que as derivadas parciais são as taxas de variação da função em relação a variável em que derivamos, é o quanto a função varia em relação àquela variável.