Exercícios de Derivadas Parciais pela Definição - Lista de Exercícios Resolvida

Considere a função:

Determine as derivadas parciais e .

Seja uma função de três variáveis independentes. Use a definição para encontrar para a função

Considere a função

Determine as derivadas parciais e .

Use a definição de derivada parcial como limite para calcular as derivadas parciais da função

No ponto .

Seja

Determine as derivadas parciais e .

Seja .

1. Calcule para todo .
2. Verifique se a função é ou não contínua em .

(Justifique todas as passagens.)

O objetivo deste exercício é examinar uma função de classe para a qual a tese do teorema de Schwarz falha: as derivadas parciais mistas não são iguais. Seja

1. Prove que se anula sobre os eixos e . Conclua então que e são iguais a zero.
2. Calcule e para pontos e conclua que e
3. Mostre que
4. Mostre que e conclua que as derivadas parciais mistas de não são igual em
5. Calcule para .
6. Use o item anterior para mostrar que para .
7. Conclua que é descontínua na origem e assim não é uma função de classe . Logo, a hipótese do teorema de Schwarz (a saber, é uma função de classe ) não se verifica.

Considere a função

1. A função é contínua em Justifique sua resposta.
2. Calcule as derivadas parciais e
3. Determine e para .
4. é diferenciável em ? Justifique sua resposta.

Mostre que a função:

É contínua no ponto . Determine as derivadas parciais e .

A tabela abaixo representa os valores, em alguns pontos, da função que admite derivadas parciais segundas contínuas:

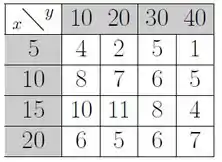
1. Estime os valores de e
2. Estime o valor de . Dica: olhe para uma tabela de estimativas de .

Observação: tais estimativas devem ser coerentes com o que vimos em sala e não meras adivinhações.

Seja a função definida por

Indique a afirmativa falsa:

1. é constante ao longo da parábola
2. é constante e igual a zero ao longo das retas e
3. é constante ao longo da reta
4. é descontínua na origem
5. As derivadas parciais e existem e são iguais a zero.

Seja

a) Esboce, no sistema de coordenadas cartesiano, as curvas e nível e de .

b) A função é contínua em ? Justifique.

c) Determine, caso exista, .

Considere a função real de duas variáveis reais dada por

1. Em quais pontos admite derivadas parciais de primeira ordem? Determine e nestes pontos.
2. Há pontos nos quais não possui derivadas parciais? Justifique.

Seja

1. Faça um esboço do conjunto

2. Determine se a função é contínua na origem.

3. Calcule, se existirem, as derivadas parciais e .