Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 15.9 - Ex. 9
Determine a imagem do conjunto sob a transformação dada.
é a região triangular com vértices , , ;
Passo 1
Faaala, beleza?
Nessa questão precisamos determinar a imagem de um conjunto sob uma transformação.
Basicamente, a ideia é essa:
Se a gente pegar todos os pontos do conjunto e aplicar a transformação, vamos formar um novo conjunto, que vou chamar de . Essa é a imagem!
Só que a gente não precisa calcular em todos os pontos (nem da pra fazer isso). A gente só precisa calcular nos limites do conjunto , que é um triângulo no .
Passo 2
Nosso conjunto é um triângulo de vértices , , . Vamos desenhar:
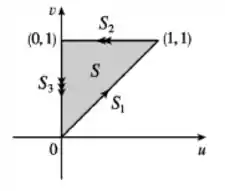
Os limites da região são três retas, que chamei de . Vamos ver uma a uma.
Primeiro vamos olhar para o lado no plano . é descrito por , e das equações dadas temos:
Substituindo na segunda equação:
Para :
Passo 3
é o segmento de reta , então:
Então temos que:
E como :
Passo 4
é o segmento de reta , então:
Vamos ficar com:
Como :
Passo 5
As imagens dos nossos limites de ficam:
Desenhando essas curvas, descobrimos quem é :
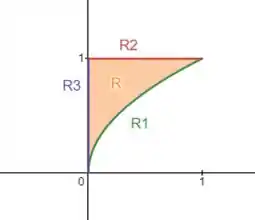
A imagem de é a região entre as curvas (), () e o eixo ().
Resposta
A região entre as curvas , e o eixo .