Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Guidorizzi - Vol 3- Ed: 5º - Capítulo 4.2 - Ex. 5

Passo 1

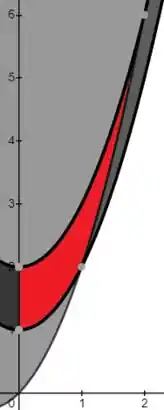
Dado as informações do conjunto A , tem-se que ele representa a região limitada pelas parábolas mostrado no seguinte esboço:

Neste caso, fazendo a substituição de variáveis indicada no enunciado, tal que:

u = x

v = y - x^2

Tem-se que:

Quando y >= 1 + x^2 -> v >= 1

Quando y <= 2 + x^2 -> v <= 2

Quando x >= 0 -> u >= 0

Quando y >= x + x^2 -> v >= x :. u <= v

Passo 2

Com isso, conclui-se que o novo conjunto formado pelas variáveis novas u e v é representado por:

(u , v) = phi (x , y) = A_n o v o

A_n o v o = phi (A) = {(u , v) in R^2 | 1 <= v <= 2 , 0 <= u <= v}

Ou:

phi (A) = {(u , v) in R^2 | 1 <= v <= 2 , v >= u e u >= 0}

Que é igual ao conjunto B . Logo:

B = A_n o v o = phi (A)

Passo 3

Para calcular a área de A , pretende-se determinar o resultado da transformação:

d x d y = |(del (x , y))/(del (u , v))| d u d v

Então:

(del (x , y))/(del (u , v)) = |[[(del x)/(del u),(del x)/(del v)],[(del y)/(del u),(del y)/(del v)]]| = |[[1,0],[2,u,1]]| = 1

|(del (x , y))/(del (u , v))| = 1

Portanto:

d x d y = d u d v

Passo 4

Visto que d x d y = d u d v , então ao substituir a variável no cálculo da área pela integral dupla:

A_A = int int_A d x d y = int_1^2 [int_0^v d u] d v

Tal que:

int_1^2 [int_0^v d u] d v = int int_B d u d v = Á r e a d e B

Portanto:

A_A = A_B

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Utilize a transformação dada para calcular a integral. ∬ R x 2 - x y + y 2 d A , onde R é a região delimitada pela elipse x 2 - x y + y 2 = 2 ; x = 2 u - 2 3 v , y = 2 u + 2 3 v
Determine a imagem do conjunto S sob a transformação dada. S = u , v | 0 ≤ u ≤ 3,0 ≤ v ≤ 2 ; x = 2 u + 3 v , y = u - v
Utilize a transformação dada para calcular a integral. ∬ R x - 3 y d A , onde R é a região triangular de vértices 0,0 , 2,1 e 1,2 ; x = 2 u + v , y = u + 2 v
Determine o jacobiano da transformaçãox = 5 u - v , y = u + 3 v
Determine o jacobiano da transformação.x = u + 4 v , y = 3 u - 2 v