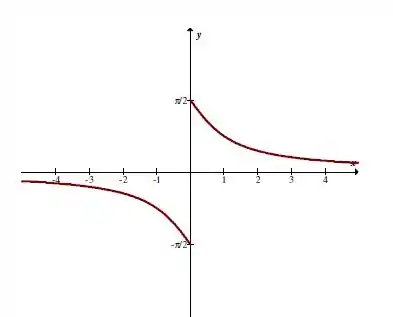
Determine limites à direita e à esquerda da função quando .
Passo 1
Para o limite dado de , estamos analisando a função da direita para a esquerda ao longo do eixo .
Assim, podemos escrever que:
Passo 2
De forma análoga, para o limite dado de , estamos analisando a função da esquerda para a direita ao longo do eixo .
Assim, podemos escrever que:
Passo 3
Esses resultados são melhores visualizados quando analisamos o gráfico da função, que é mostrado abaixo:
Resposta
Ei, a resposta está no passo a passo :)