Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 15.7 - Ex. 42

Determine a massa e o centro de massa do sólido dado E com função densidade dada ρ .

E é o tetraedro limitado pelos planos x = 0 ,   y = 0 ,   z = 0 ,   x + y + z = 1

ρ x , y , z = y

Passo 1

Podemos colocar a variação de x como

0 ≤ x ≤ 1 - y - z

E no plano y z temos a intersecção do plano x + y + z = 1 quando x = 0

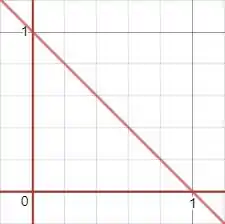
As variações podem ser colocadas como

0 ≤ z ≤ 1 - y

0 ≤ y ≤ 1

Passo 2

A massa é dada por

m = ∭ E ρ   d V

Então

m = ∫ 0 1 ∫ 0 1 - y ∫ 0 1 - y - z y   d x d z d y

= ∫ 0 1 ∫ 0 1 - y y 1 - y - z   d z d y = ∫ 0 1 - y 1 - y - z 2 2 0 1 - y d y

= ∫ 0 1 - y 1 - y - ( 1 - y ) 2 2 + y 1 - y 2 2 d y

= ∫ 0 1 y 1 - y 2 2 d y = ∫ 0 1 y - 2 y 2 + y 3 2 d y

= y 2 4 - y 3 3 + y 4 8 0 1 = 1 4 - 1 3 + 1 8

= 6 - 8 + 3 24

m = 1 24

Passo 3

O centro de massa é dado por ( x - , y - , z - ) onde

x - = M y z m                     y - = M x z m                     z - = M x y m

Calculando os momentos, primeiro no plano y z

M y z = ∭ E x   ρ   d V = ∫ 0 1 ∫ 0 1 - y ∫ 0 1 - y - z x y   d x d z d y

= ∫ 0 1 ∫ 0 1 - y y 1 - y - z 2 2 d z d y = ∫ 0 1 y - 1 - y - z 3 6 0 1 - y d y

= ∫ 0 1 y 1 - y 3 6 d y = ∫ 0 1 y - 3 y 2 + 3 y 3 - y 4 6 d y

= y 2 12 - y 3 6 + y 4 8 - y 5 30 0 1 = 1 12 - 1 6 + 1 8 - 1 30

= 10 - 20 + 15 - 4 120 = 1 120

M y z = 1 120

Como as variáveis x e z são simétricas na região e na função densidade

M x y = 1 120

No plano x z

M x z = ∭ E y   ρ   d V = ∫ 0 1 ∫ 0 1 - y ∫ 0 1 - y - z y 2   d x d z d y

= ∫ 0 1 ∫ 0 1 - y y 2 1 - y - z   d z d y = ∫ 0 1 y 2 - 1 - y - z 2 2 0 1 - y d y

= ∫ 0 1 y 2 1 - y 2 2 d y = ∫ 0 1 y 2 - 2 y 3 + y 4 2 d y

= y 2 6 - y 4 4 + y 5 10 0 1 = 1 6 - 1 4 + 1 10

= 10 - 15 + 6 60

M x z = 1 60

Passo 4

Calculando as coordenadas do centro de massa

x - = M y z m = 1 120 1 24 = 1 5

y - = M x z m = 1 60 1 24 = 2 5

z - = M x y m = 1 120 1 24 = 1 5

Então temos

x - , y - , z - = 1 5 , 2 5 , 1 5

Resposta

m = 1 24

x - , y - , z - = 1 5 , 2 5 , 1 5

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Encontre o centro de massa do sólido E com a dada função de densidade ρ .
Encontre o centro de massa do sólido E com a dada função de densidade ρ .
Estabeleça, mas não calcule, as expressões integrais para (a) a massa, (b) o centro de massa e (c) o momento de inercia em relação ao eixo z.O sólido do exercício 19; ρ x , y , z = x 2 + y 2
Estabeleça, mas não calcule, as expressões integrais para (a) a massa, (b) o centro de massa e (c) o momento de inercia em relação ao eixo z.O hemisfério x 2 + y 2 + z 2 ≤ 1 ,z ≥ 0 ; ρ x , y , z = x 2
Calcular a massa dos sólidos limitados pelas superfícies dadas, considerando a densidade de massa igual a 4 k g m 3 . z = x 2 + y 2 z = 9 - x 2 - y 2