Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 15.7 - Ex. 43
Determine os momentos de inércia para um cubo com densidade constante k e lados de comprimento se um vértice está localizado na origem e três arestas estão nos eixos coordenados.
Passo 1
Fala pessoal, tudo na paz com vocês? Borá la começar!
O enunciado pede para determinar os momentos de inercia para um cubo que possui densidade constante e lados com comprimento , sendo que um vértice esta na origem e três arestas sobre os eixos coordenados.
E agora??
Nosso primeiro objetivo é fazer um esboço tridimissencional para conhecer nossa região de integração. Com isso vamos perceber que a simetria entre os eixos, pois se trata de um cubo de lado .
Precisamos lembrar da fórmula do momento de inércia. Ele tem essa cara:
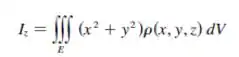
Como sabemos que o cubo tem simetria, pois todos os lados são iguais a ...logo, nosso momento de inércia em relação aos eixos , e vão ser iguais.
Para reduzir nossos cálculos, podemos obter apenas o .
Passo 2
Vamos começar esboçando nossa região.
Ela vai ter essa cara:
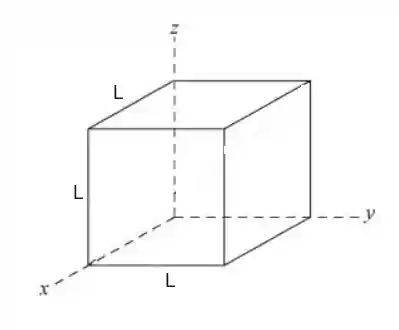
Como o cubo possui simetria em relação aos eixos , e , o momento de inercia vai ser igual em relação a esses eixos.
Passo 3
Sabendo da simetria, podemos calcular apenas o .
Logo, temos a seguinte integral para ser calculada.
Onde,
é a densidade
Do enunciado, sabemos que a densidade é constante é vale .
Avaliando o esboço da região, sabemos que os intervalos são:
Então, vamos ter que resolver a seguinte integral.
Passo 4
Importante lembrar, que começamos a integrar de dentro para fora.
Integrando em e aplicando os limites de integração, vamos ter:
Agora vamos integrar em dy e também aplicar os limites de integração. Logo:
Por fim, ficamos com uma integral simpes em . Integrando e aplicando os limites de integração temos:
Pela simetria sabemos que:
Logo, temos: