Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Guidorizzi - Vol 3- Ed: 5º - Capítulo 5.7 - Ex. 4

Calcule o cilindro homogêneo x - a 2 + y 2 ≤ a 2 e 0 ≤ z ≤ h

  1. Calcule o momento de inércia em relação à reta x = a e y = 0
  2. Calcule o momento de inércia em relação ao eixo O z .

Passo 1

Vamos olhar para o início da nossa seção 5.7 e nos atentar para a seguinte relação

I = ∭ B r 2 d m

Que é definido como nosso momento de inércia, na qual d m = δ x , y , z d x   d y   d z e δ x , y , z é nossa densidade volumétrica. Assim agora precisamos só aplicarmos nossa equação. Claro que estou aqui para ajuda-los ...

Passo 2

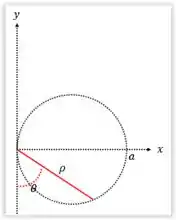
a) Olhando para nossa equação, temos um cilindro de raio a , centrado em a , 0 e de altura h . Assim temos que, o que o exercício nos pede, é para calcular nosso cilindro em relação ao seu centro. Temos que a distância de qualquer ponto do nosso cilindro do seu centro é dada por r , tal que, r 2 = x - a 2 + y 2 e como nosso cilindro é homogêncio, temos que δ x , y , z = k

Como lidamos com um cilindro é mais fácil resolvemos nosso integral usando coordenada cilíndricas, dãããããã... Então fazemos

x - a = ρ cos ⁡ θ

y = ρ   s e n   θ

z = z

Desta forma temos que 0 ≤ ρ ≤ a e 0 ≤ θ ≤ 2 π o que confia, torna a integral bem mais fácil. Outra coisa importante que nunca podemos esquecer, é que quando fazemos uma transformação de coordenada, devemos calcular o jacobiano, que no caso de coordenadas cilíndricas é ρ . Assim temos

I = k ∫ 0 a ∫ 0 2 π ∫ 0 h ρ 2   ρ   d z   d θ   d ρ

Que não é um integral difícil, não concorda?

I = k ρ 4 4 0 a 2 π h = k π a 4 h 2

Como para nosso cilindro temos que k = M / V

Temos que

M = k V = k π a 2 h

Assim ficamos com

I = M a 2 2

Passo 3

b) Aqui queremos calcular o momento de icércia com relação ao eixo O z . Desta forma vamos apelar a nosso amigo pitagora e tomar que qualquer ponto dista do eixo z por r 2 = x 2 + y 2 .

Usando nossas coordenadas cilíndricas, temos

x = ρ cos ⁡ θ

y = ρ   s e n   θ

z = z

Assim temos que

x - a 2 - y 2 = a 2 → ρ 2 - 2 a ρ cos ⁡ θ = 1

ρ = 2 a cos ⁡ θ

Assim temos que

0 ≤ ρ ≤ 2 a cos ⁡ θ ,   - π / 2 ≤ θ ≤ π / 2 ,   0 ≤ z ≤ h

Com isso ficamos com

I = k ∫ - π / 2 π / 2 ∫ 0 h ∫ 0 2 a cos ⁡ θ ρ 2   ρ   d ρ   d θ   d z

Em z nossa integral da h e agora vamos resolver para ρ

Então temos

I = k h   ∫ - π / 2 π / 2 ρ 4 4 0 2 a cos ⁡ θ d θ = 8 k h a 4   ∫ - π / 2 π / 2 cos 4 ⁡ θ   d θ

Como cosseno é uma função par e estamos integrando em um intervalo simétrico, ficamos com

I = 8 a 4 k h ∫ 0 π / 2 cos 4 ⁡ θ   d θ

E agora como integra o cosseno a quarta?

Vamos fazer que cos 4 ⁡ θ = cos 3 ⁡ θ cos ⁡ θ . Assim usando integral por partes ( u   d v ) , temos

∫ 0 π / 2 cos 4 ⁡ θ d θ = ∫ 0 π / 2 cos 3 ⁡ θ cos ⁡ θ   d θ = cos 3 ⁡ θ   s e n   θ 0 π 2 - ∫ 0 π 2 - 3 cos 2 ⁡ θ   s e n 2 θ   d θ

A primeira parte da integral claramente é nula, visto que cos ⁡ π 2 = 0 e s e n   0 = 0 . Assim nos sobra que

∫ 0 π / 2 cos 4 ⁡ θ d θ = ∫ 0 π 2 3 cos 2 ⁡ θ   s e n 2 θ   d θ = 3 ∫ 0 π 2 cos ⁡ θ   s e n   θ 2   d θ

E lembrando nossas relações trigonométricas, ou deduzindo a partir de s e n   ( 2 θ ) , temos que

cos ⁡ θ   s e n   θ = s e n   ( 2 θ ) 2

Assim ficamos com

3 4 ∫ 0 π / 2 s e n 2 2 θ d θ

Outra relação importante que devemos lembrar dedizindo a partir de cos ⁡ 2 θ é

s e n 2 θ = 1 - cos ⁡ 2 θ 2

Assim novamos nossa integral se resume em

3 8 ∫ 0 π / 2 1 - cos ⁡ 4 θ d θ

Desta forma temos por fim

3 8 θ - s e n 4 θ 4 0 π / 2 = 3 π 16

E depois de muito sofrer neste nosso item, temos

I = 8 a 4 k h 3 π 16 = 3 π a 4 k h 2 = 3 2 M a 2

Resposta

  1. I = M a 2 2
  2. I = 3 2 M a 2
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine os momentos de inércia para um cubo com densidade constante k e lados de comprimentoL se um vértice está localizado na origem e três arestas estão nos eixos coordenados.
Determine os momentos de inércia do tijolo retangular de dimensões a , b e c , massa M e densidade constante se o centro do tijolo está na origem e suas arestas são paralelas aos eixos coordenados.
Calcular o momento de inércia do hemisfério x 2 + y 2 + z 2 ≤ 1 ,x ≥ 0 em relação ao eixo y . A densidade no ponto P ( x , y , z ) é proporcional à distância de P ao plano y z .
Calcular o momento de inércia em relação ao eixo dos x do sólido delimitado por z = x 2 + y 2 e z = 4 . A densidade de massa em um ponto P x , y , z é dada por x 2k g / m 3 .
Calcular o momento de inércia em relação aos eixos coordenados do sólido delimitado por z = 4 - x 2 - y 2 e z = 0 , sabendo que a densidade de massa em um ponto P é proporcional à distância de P ao pl