Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Guidorizzi - Vol 3- Ed: 5º - Capítulo 5.7 - Ex. 3

Considere o cubo 0 ≤ x ≤ 1 , 0 ≤ y ≤ 1 e 0 ≤ z ≤ 1 e suponha que a densidade no ponto ( x , y , z ) seja x :

  1. Calcule o momento de inércia em relação ao eixo O z .
  2. Calcule o centro de Massa

Passo 1

Vamos olhar para o início da nossa seção 5.7 e nos atentar para a seguinte relação

I = ∭ B r 2 d m

Que é definido como nosso momento de inércia, na qual d m = δ x , y , z d x   d y   d z e δ x , y , z é nossa densidade volumétrica. Assim agora precisamos só aplicarmos nossa equação. Claro que estou aqui para ajuda-los ...

Já o centro de massa, vamos calcular tomando a seguinte relação

s C = ∭ s d m ∭ d m

Onde s é nossa coordenada x , y , z .

Mas chega de teoria e vamos para a prática.

Passo 2

  1. Como estamos lidando com um cubo, temos por consequência que 0 ≤ x ≤ 1 , 0 ≤ y ≤ 1 e 0 ≤ z ≤ 1 . Assim como nos pede, vamos calcular o momento em relação ao eixo z .

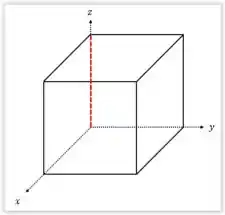
    2. Desta forma, lembrando do nosso famoso pitagoras, ele ira dizer que, qualquer ponto dista de z , por x 2 + y 2 , assim tomando que nosso cubo tem densidade igual a δ x , y , z = x , temos que

    I = ∫ 0 1 ∫ 0 1 ∫ 0 1 x 2 + y 2   x   d x   d y   d z

    Integrando primeiro em z , temos

    I =   ∫ 0 L ∫ 0 L x 2 + y 2 x   d x   d y

    Ou seja, como a integral é de 0 à 1 , temos que nossa integral tripla se simplifica em uma integral dupla.

    Integrando em x

    I =   ∫ 0 1 x 4 4 + y 2 x 2 2 0 1 d y = ∫ 0 1 1 4 + y 2 2 d y

    E por fim, vamos integrar em y

    I = 1 4 y + y 3 6 0 1 = 1 4 + 1 6 = 5 12

    Interessante que não foi um problema difícil de resolvermos. Entrentando agora indo pro item (b) iremos ter mais trabalho.

    Passo 3

  2. Se fossemos começar calculando x C , teríamos que resolver

x C = ∭ x d m ∭ d m

Assim, vamos primeiro resolver a integral de nominador para todas as coordenada e por fim resolvermos uma única vez a integral do denominador

Logo em x temos

∫ 0 1 ∫ 0 1 ∫ 0 1 x   x   d x   d y   d z = ∫ 0 1 ∫ 0 1 ∫ 0 1 x 2   d x   d y   d z

Tanto em y e z as integrais são 1 .

Então ficamos com a integral somente em x que temos como resultado 1 / 3 .

Já para y e para z temos simetria na integral, então

∭ y   d m = ∭ z   d m = ∫ 0 1 ∫ 0 1 ∫ 0 1 y   x   d x   d y   d z = z 0 1 x 2 2 0 1 y 2 2 0 1 = 1 4

E a integral de massa é definida no denominador por

∭ d m = ∫ 0 1 ∫ 0 1 ∫ 0 1 x   d x   d y   d z = x 2 2 0 1 = 1 2

Desta forma fica fácil concluir que

x C = 1 / 3 1 / 2 = 2 / 3

y C = z C = 1 / 4 1 / 2 = 1 / 2

Assim temos que nosso centro de massa é o ponto

2 3 , 1 2 , 1 2

Resposta

  1. 5 / 12
  2. 2 3 , 1 2 , 1 2  
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

(Teorema de Steiner ou dos iexos paralelos). Seja I c m o momento de inércia em relação a um eixo que passa pelo centro de massa de um corpo e I o momento de inércia em relação a um eixo paralelo, a u
Calcule o momento de inércia de um sólido homogêneo com a forma de um cone circular reto de altura h e o raio da base R , em relação a um eixo passando pelo vértice e perpendicular ao eixo do cone.
Calcule o momento de inércia do cubo homogêncio de aresta L , em relação a um eixo que contém uma das arestas.
Calcule o momento de inércia de uma esfera homogênea de raio R , em relação a um eixo cuja distância ao centro seja h
Calcule o momento de inércia do corpo homogêneo x + y + z ≤ 4 , x ≥ 0 , y ≥ 0 e z ≥ 0 , em relação ao eixo z .