Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 11.1 - Ex. 54
Determine se a sequência converge ou diverge. Se ela convergir, encontre o limite.
Passo 1
Hey, galera! Como vocês estão?
Aqui não temos uma fórmula geral de pra tentar calcular o limite, então temos que observar o padrão dos primeiros termos.
Parece meio estranha a sequência, porque ela não é crescente nem decrescente, ela parece que aumenta e diminui, aumenta e diminui. Vamos usar um gráfico para ajudar na análise desse comportamento.
No final, vamos precisar encontrar o limite dessa sequência caso ela converja.
Passo 2
Vamos analisar o gráfico da nossa sequência. A nossa sequência parece ter “duas partes”, uma mais acima e uma mais embaixo, com termos alternadamente variando de uma para a outra. Vamos tentar separar essas nossas sequências usando os termos que nos foram dados:
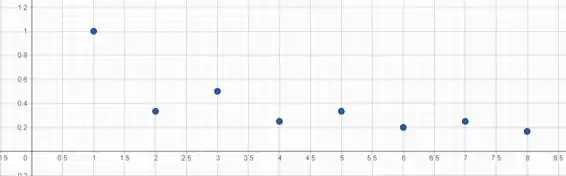
Bom, a gente pode dividir essa sequência em duas subsequências, ao pegar termos alternados:
Agora, olha que interessante: a primeira sequência pode ser escrita como:
E a segunda:
Passo 3
Vamos calcular o limite das duas séries para entendermos se há convergência:
Para a outra sequência:
Já que com os denominadores se tornam muito grandes, fazendo o termo todo muito pequeno.
Como nossas duas subsequências convergem para 0 podemos dizer que nossa sequência também converge para 0.
Resposta
Sequência convergente para 0.