Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 14.3 - Ex. 6
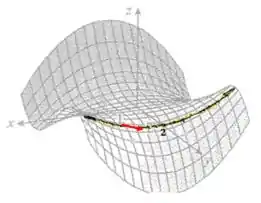
6- Determine os sinais das derivadas parciais da função cujo gráfico está mostrado.
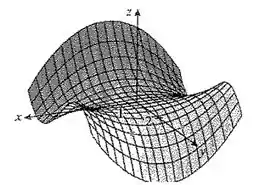
Passo 1
Fala galerinha. De boa?
O objetivo dessa questão é determinar os sinais das derivadas parciais da função em um ponto. Você se lembra o que são derivadas parciais?
Primeiramente, vamos lembrar que derivadas são taxas de variação.
E as derivadas parciais são derivadas com relação a uma variável, quando consideramos a outra como constante. Ou seja, esse termo é a variação da função na direção do eixo , ou seja, com constante, no ponto em que e .
como a função varia em relação a e E precisamos fazer isso observando o gráfico tridimensional. A análise da inclinação do gráfico em direções específicas fornece os sinais das derivadas parciais. Mas temos que lembrar de mais um conceito: derivada positiva significa que a curva é crescente e derivada negativa significa que a curva é decrescente.
Para resolver vamos fazer o seguinte, para cada ponto, devemos observar a variação da altura (eixo ) ao longo dos eixos oue e, a partir disso, vamos descobrir se as derivadas parciais são positivas ou negativas.
Vamos começar a analisar!
Passo 2
a)
Se traçarmos uma reta paralela ao eixo em nós vemos que a função forma uma parábola com ponto mínimo em , como mostra a imagem a seguir.
logo se formos pegar o ponto e andarmos na direção positiva de vemos que diminui, logo tem sinal negativo.
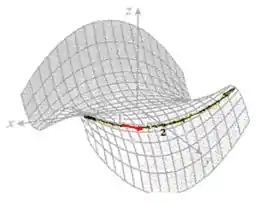
Agora se formos pegar o ponto e andarmos na direção positiva de vemos que diminui, logo tem sinal negativo.
Passo 3
Na letra B, vamos traçar uma reta paralela em em , e nela conseguimos ver uma espécie de função ímpar (como um ) e que se andarmos na direção de vemos que o valor de tende a diminuir, logo é negativo.
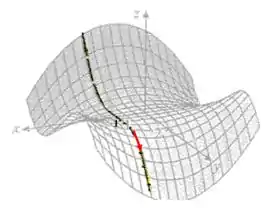
Passo 4
Na letra C, vamos analisar as concavidades, a concavidade em . A parábola vista em aponta para cima, o que nos diz que tem sinal positivo.
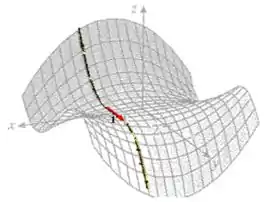
Passo 5
E por último na letra D, assim como a concavidade da função na reta em aponta para baixo, fazendo com que tenha sinal negativo.
