Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Um curso de Cálculo Volume 2 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 10.1 - Ex. 26

Seja f x , y = 2 x y 2 x 2 + y 4 s e   x , y ≠ 0,0 0 s e   x , y = 0,0 e seja γ t = t , t , z ( t ) , t ∈ R uma curva cuja imagem está contida no gráfico de f . Seja T a reta tangente a γ em γ 0 . Mostre que T não está contida no plano da equação

z - f 0,0 = ∂ f ∂ x 0,0 x - 0 + ∂ f ∂ y 0,0 y - 0

Passo 1

É dada uma função f de duas variáveis e uma curva γ contida em f .

Note que, como γ DEVE pertencer ao gráfico da f , deve existir a seguinte relação entre as componentes de γ :

z t = 2 t 3 t 2 + t 4 = 2 t 1 + t 2 s e   t ≠ 0 z t = 0 s e   t = 0

Agora, vamos derivar a relação acima em relação a t e deixar o resultado anotado:

z ' t = 2 - 2 t 2 1 + t 2 2 s e   t ≠ 0 z ' t = 0 s e   t = 0

Passo 2

Agora, para determinar a reta tangente a γ em γ 0 , recorremos à figura abaixo:

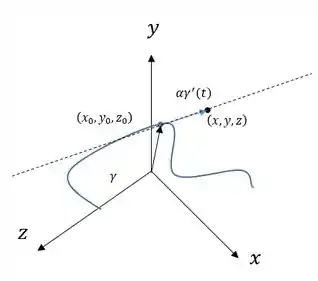
Note que, pela figura, um ponto qualquer x , y , z sobre a reta tangente será dado pela soma do vetor ponto de referência, no caso 0,0 , z 0 , com o vetor α γ ' , para algum número α . Escrevendo isto em forma de equação, temos:

x , y , z = 0,0 , z 0 + α γ '

Mas, usando as relações que deixamos anotadas para γ ' = 1,1 , z ' , a equação acima fica

x , y , z = 0,0 , z 0 + α 1,1 , 2 s e   t ≠ 0 x , y , z = 0,0 , z 0 + α 1,1 , 0 s e   t = 0

Estas equações vetoriais representam as seguintes igualdades:

x = α y = α z = z 0 + 2 α s e   t ≠ 0 x = α y = α z = z 0 s e   t = 0

Que é a equação da reta tangente no ponto!

Passo 3

Seja T a reta obtida no item anterior. Devemos mostrar que esta reta satisfaz a equação:

z - f 0,0 = ∂ f ∂ x 0,0 x - 0 + ∂ f ∂ y 0,0 y - 0

Mas, nesta expressão,

∂ f ∂ x 0,0 = ∂ 2 x y 2 x 2 + y 4 ∂ x 0,0 = 2 y 2 x 2 + y 4 - 4 x 2 y 2 x 2 + y 4 2 0,0 = 2 y 2 y 4 - x 2 x 2 + y 4 2 0,0

Dá pra mostrar que o limite acima fornece ∂ f ∂ x 0,0 = 0 . E, analogamente, ∂ f ∂ y 0,0 = f 0,0 = 0 .

Ou seja, a equação do plano tangente se reduz a:

z = 0

Ou seja, o próprio plano x - y .

Agora nos perguntamos: está a reta tangente T contida no plano dado? Bem, se estivesse, cada ponto da reta deveria ter z = 0 para pontos ( x , y ) na origem e nas proximidades desta, o que vemos que não acontece, pois muito perto de 0 a reta dá um pulo.

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

80. A temperatura em um ponto x ,y de uma chapa de metal é dada por T x ,y = 60 / ( 1 + x 2 + y 2 ) , onde T é medido em ° C e x , y em metros. Determine a taxa de variação da temperatura no ponto 1 ,
93. Se f x , y = x x 2 + y 2 - 3 / 2 e s e n x 2 y , determine f x ( 1,0 ) . [Sugestão: Em vez de achar f x ( x , y ) primeiro, observe que é mais fácil utilizar a Equação 1 ou a Equação 2.]