Enunciado
Cálculo - Um curso de Cálculo Volume 2 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 10.1 - Ex. 23
Seja e seja , , uma curva cuja imagem está contida no gráfico de .
a) Determine .
b) Esboce os gráficos de e .
c) Determine a reta tangente a no ponto .
d) Seja a reta tangente do item ; mostre que está contida no plano de equação
Passo 1
É dada uma função de duas variáveis e uma curva , e precisamos esboçar o gráfico da , assim como obter outras informações.
Primeiramente, no item a), é dado , onde devemos identificar qual a função que faça com que pertença ao gráfico da .
Mas ué, o é nada menos que um e o é nada mais que um . Ou seja, devemos ter:
Dai,
Passo 2
Para esboçar o gráfico, devemos analisar um pouco o jeitão da , vendo seus valores para alguns ponto, por exemplo. Ou, melhor, podemos notar simplesmente que a representa a equação de um paraboloide , que a esta altura do campeonato sabemos desenhar muito bem!
Já para determinar o gráfico de basta notar que esta curva só existe para , ou seja, esa curva é nada mais do que a interseção do plano vertical com o paraboloide da .
Com todo esse raciocínio, o esboço fica o seguinte:
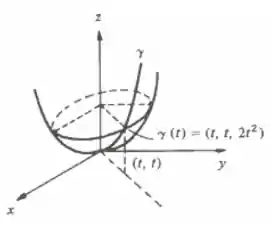
Passo 3
Note que o ponto em refere-se a .
Agora, para determinar a reta tangente a no ponto , recorremos à figura abaixo:
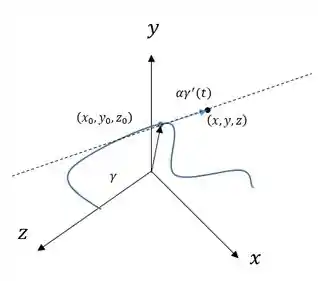
Note que, pela figura, um ponto qualquer sobre a reta tangente será dado pela soma do vetor ponto de referência, no caso , com o vetor , para algum número . Escrevendo isto em forma de equação, temos:
Mas, sendo , temos , ou, para , ficamos com:
Esta equação vetorial representa três equações:
Que é a equação da reta tangente no ponto!
Passo 4
Seja a reta obtida no item anterior. Devemos mostrar que esta reta satisfaz a equação:
Mas, nesta expressão,
E também
Assim, como , a equação que queremos testar fica
Agora, será que nossa reta se encaixa nesta equação? Bem, basta substituir o da reta ali para sabermos ao certo:
Simplificando, esta equação fornece , o que basta para provar que realmente está contida no plano dado.
Resposta
a)
b)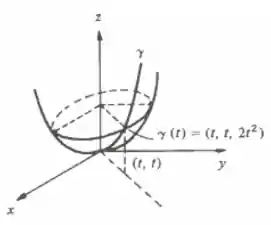 
c)